题目内容
已知向量
，
满足|
|=1，|
|=2，
与
的夹角为60°，则（2
-
）•（
+
）= ．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
考点：数量积表示两个向量的夹角,平面向量数量积的运算
专题：平面向量及应用
分析：由已知可求
•
，将所求展开，利用向量的平方等于模的平方可求．
| a |
| b |
解答：
解：∵向量
，
满足|
|=1，|
|=2，
与
的夹角为60°，
∴
•
=|
||
|cos60°=1×2×
=1，
∴（2
-
）•（
+
）=2|
|2-|
|2+
•
=2-4+1=-1；
故答案为：-1．
| a |
| b |
| a |
| b |
| a |
| b |
∴
| a |
| b |
| a |
| b |
| 1 |
| 2 |
∴（2
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
故答案为：-1．
点评：本题考查了向量的数量积的运算；对于非坐标的向量求数量积，一般借助于已知的向量的模以及数量积解答．
练习册系列答案
新思维寒假作业系列答案
相关题目
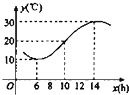某地一填从6时至14时的温度函数变化曲线近似满足y=Asin（ωx+φ）+b（|φ|＜π）