题目内容
函数f(x)=
+cosx,x∈[0,
]的最大值是 .
| x |
| 2 |
| π |
| 2 |
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:由已知得f′(x)=
-sinx,由此利用导数性质能求出函数f(x)=
+cosx,x∈[0,
]的最大值.
| 1 |
| 2 |
| x |
| 2 |
| π |
| 2 |
解答:
解:∵f(x)=
+cosx,
∴f′(x)=
-sinx,
由f′(x)=0,得x=
,
∵f(0)=1,f(
)=
+
,f(
)=
,
∴函数f(x)=
+cosx,x∈[0,
]的最大值是f(
)=
+
.
故答案为:
+
.
| x |
| 2 |
∴f′(x)=
| 1 |
| 2 |
由f′(x)=0,得x=
| π |
| 6 |
∵f(0)=1,f(
| π |
| 6 |
| π |
| 12 |
| ||
| 2 |
| π |
| 2 |
| π |
| 4 |
∴函数f(x)=
| x |
| 2 |
| π |
| 2 |
| π |
| 6 |
| π |
| 12 |
| ||
| 2 |
故答案为:
| π |
| 12 |
| ||
| 2 |
点评:本题考查函数的最大值的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
相关题目

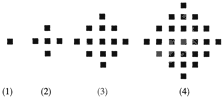 某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.