题目内容
命题“任何一个实数与其相反数的和都是零”的否定是（ ）
| A、任何一个实数与其相反数的和都不是零 |
| B、任何一个实数与其相反数的差都是零 |
| C、存在一个实数与其相反数的差都是零 |
| D、存在一个实数与其相反数的和不为零 |
考点：命题的否定
专题：简易逻辑
分析：全称命题的否定是特称命题写出结果即可．
解答：
解：因为全称命题的否定是特称命题，
所以命题“任何一个实数与其相反数的和都是零”的否定是：存在一个实数与其相反数的和不为零．
故选：D．
所以命题“任何一个实数与其相反数的和都是零”的否定是：存在一个实数与其相反数的和不为零．
故选：D．
点评：本题考查命题的否定，特称命题与全称命题的否定关系，基本知识的考查．
练习册系列答案
相关题目
在极坐标系中，由三条直线θ=0，θ=
，ρcosθ+ρsinθ=1围成图形的面积是（ ）
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
36°化为弧度制为（ ）
A、
| ||
B、
| ||
| C、5 | ||
| D、5π |
在半径不等的两个圆内，1弧度的圆心角（ ）
| A、所对弧长相等 |
| B、所对的弦长相等 |
| C、所对弦长等于各自半径 |
| D、所对的弧长等于各自半径 |
已知函数f（x）是偶函数，且f（x）在[0，+∞）是增函数，如果不等式f（a）≤f（1）恒成立，则实数a的取值范围是（ ）
| A、（-∞，1） |
| B、（-∞，1）∪[0，1] |
| C、（-∞，-1]∪[1，+∞） |
| D、[-1，1] |
过双曲线
-y2=1的右焦点F作直线l交双曲线于A、B两点，|AB|=4，则这样的直线l有（ ）
| x2 |
| 2 |
| A、1条 | B、2条 | C、3条 | D、4条 |
如图所示的程序框图，它的输出结果是（ ）
| A、3 | B、4 | C、5 | D、6 |
设向量
=（2，3），
=（-1，2），若m
+
与
-2
平行，则实数m等于（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、-2 | ||
| B、2 | ||
C、
| ||
D、-
|
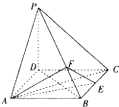如图，ABCD是正方形，PD⊥平面ABCD，点E是BC中点，点F在PB上，且PE=2FB．