题目内容
10.已知函数f(x)=x2-kx-8在区间[2,5]上具有单调性,则实数k的取值范围是(-∞,4]∪[10,+∞).分析 函数f(x)=x2-kx-8在[2,5]上具有单调性可知[2,5]在对称轴一侧,列出不等式解出.
解答 解:f(x)图象的对称轴是x=$\frac{k}{2}$,
∵f(x)=x2-kx-8在[2,5]上具有单调性,
∴$\frac{k}{2}$≤2或$\frac{k}{2}$≥5.
解得k≤4或k≥10.
故答案为(-∞,4]∪[10,+∞).
点评 本题考查了二次函数的单调性与对称轴的关系,找到区间[1,5]与对称轴的关系是解题关键,是基础题.

练习册系列答案
相关题目
20.某三棱锥的三视图如图所示,则该三棱锥的表面积是( )
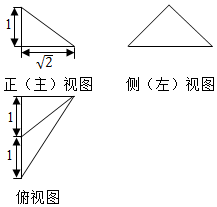

| A. | 2+2$\sqrt{2}$ | B. | 2+$\sqrt{2}$ | C. | 4+2$\sqrt{2}$ | D. | 4+$\sqrt{2}$ |
18. 已知甲、乙两名同学在某项测试中得分成绩的茎叶图如图所示,x1,x2分别表示知甲、乙两名同学这项测试成绩的众数,s12,s22分别表示知甲、乙两名同学这项测试成绩的方差,则有( )
已知甲、乙两名同学在某项测试中得分成绩的茎叶图如图所示,x1,x2分别表示知甲、乙两名同学这项测试成绩的众数,s12,s22分别表示知甲、乙两名同学这项测试成绩的方差,则有( )
 已知甲、乙两名同学在某项测试中得分成绩的茎叶图如图所示,x1,x2分别表示知甲、乙两名同学这项测试成绩的众数,s12,s22分别表示知甲、乙两名同学这项测试成绩的方差,则有( )
已知甲、乙两名同学在某项测试中得分成绩的茎叶图如图所示,x1,x2分别表示知甲、乙两名同学这项测试成绩的众数,s12,s22分别表示知甲、乙两名同学这项测试成绩的方差,则有( )| A. | x1>x2,s12<s22 | B. | x1=x2,s12>s22 | C. | x1=x2,s12=s22 | D. | x1=x2,s12<s22 |
15.在长方体ABCD-A1B1C1D1中,$\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{D{D_1}}$=( )
| A. | $\overrightarrow{{D_1}{B_1}}$ | B. | $\overrightarrow{{D_1}B}$ | C. | $\overrightarrow{D{B_1}}$ | D. | $\overrightarrow{B{D_1}}$ |
2.设f(x)是定义域为R且最小正周期为2π的函数,且有f(x)=$\left\{\begin{array}{l}{sinx,0≤x≤π}\\{cosx,-π<x<0}\end{array}\right.$,则f(-$\frac{13π}{4}$)=( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | 0 | D. | 1 |
20.在如下程序框图中,已知f0(x)=sinx,则输出的结果是( )


| A. | sinx | B. | cosx | C. | -sinx | D. | -cosx |
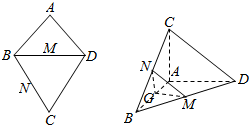 如图,AB=AD,∠BAD=90°,M,N,G分别是BD,BC,AB的中点,将等边△BCD沿BD折叠到△BC′D的位置,使得AD⊥C′B.
如图,AB=AD,∠BAD=90°,M,N,G分别是BD,BC,AB的中点,将等边△BCD沿BD折叠到△BC′D的位置,使得AD⊥C′B.