题目内容

5．已知有相同的两焦点F1，F2的椭圆$\frac{{x}^{2}}{m}$+y2=1（m＞1）和双曲线$\frac{{x}^{2}}{n}$-y2=1（n＞0），P是它们的一个交点，则$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$等于（　　）
A．1B．$\frac{1}{2}$
C．0D．随m，n的变化而变化

分析 利用双曲线和椭圆的定义、余弦定理和三角形的面积计算公式，即可得$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$．

解答 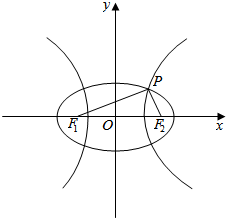解：如图所示，不妨设两曲线的交点P位于双曲线的右支上，设|PF1|=s，|PF2|=t．
由双曲线和椭圆的定义可得$\left\{\begin{array}{l}{s+t=2\sqrt{m}}\\{s-t=2\sqrt{n}}\end{array}\right.$，
解得s2+t2=2m+2n，st=m-n．
在△PF1F2中，cos∠F1PF2=$\frac{{s}^{2}+{t}^{2}-4{c}^{2}}{2st}$=$\frac{2m+2n-4（m-1）}{2m-2n}$
∵m-1=n+1，
∴m-n=2，
∴cos∠F1PF2=0，∴∠F1PF2=90°．
∴$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0．
故选：C．

点评 本题考查椭圆与双曲线方程及其几何性质及代数运算能力．熟练掌握双曲线和椭圆的定义、余弦定理和向量的数量积计算公式是解题的关键．

练习册系列答案
相关题目
17．若函数f（x）=2x3+bx2+cx+d是奇函数，定义域为[2c-3，c]，求b，c，d的值．
16．已知锐角三角形ABC中，角A，B，C所对的边分别是a，b，c，且$tanB=\frac{{\sqrt{3}sinAsinC}}{{{{sin}^2}A+{{sin}^2}C-{{sin}^2}B}}$．
（Ⅰ）求角B的大小；
（Ⅱ）若$b=\sqrt{3}$，求a+c的最大值，并求此时的三角形面积．
13．已知函数g（x）=Asin（ωx+φ）（其中A＞0，|φ|＜$\frac{π}{2}$，ω＞0）的图象如图所示，函数f（x）=g（x）+$\frac{\sqrt{3}}{2}$cos2x-$\frac{3}{2}$sin2x
（1）如果${x_1}，\;{x_2}∈（-\frac{π}{6}，\frac{π}{3}）$，且g（x1）=g（x2），求g（x1+x2）的值；
（2）当-$\frac{π}{6}$≤x≤$\frac{π}{3}$时，求函数f（x）的最大值、最小值及相应的x值；
（3）已知方程f（x）-k=0在$[0，\frac{π}{2}]$上只有一解，则k的取值集合．
20．图中是四棱台的侧面展开图的是（　　）
A．B．C．D．
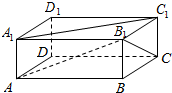10．如图所示，ABCD-A1B1C1D1是长方体，AA1=a，∠BAB1=∠B1A1C1=30°，则AB与A1C1所成的角为30°，AA1与B1C所成的角为45°．
17．在四面体OABC中，棱OA、OB、OC两两垂直，且OA=1，OB=2，OC=3，G为△ABC的重心，则$\overrightarrow{OG}$•（$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$）=$-\frac{4}{3}$．
14．若A、B、C为△ABC的三内角，且其对边分别为a、b、c．若向量$\overrightarrow{m}$=（cos2$\frac{A}{2}$，cos$\frac{A}{2}$-1），向量$\overrightarrow{n}$=（1，cos$\frac{A}{2}$+1）且2$\overrightarrow{m}$•$\overrightarrow{n}$=-1．
（1）求A的值；         
（2）若a=2$\sqrt{3}$，三角形面积S=$\sqrt{3}$，求b+c的值．
15．已知xn-1=$\frac{1}{1+\frac{1}{{x}_{n}}}$（n为1，2，3）．
（1）当x1=a时，求x2012的值；
（2）当x1=b时，求x1×x2+x2×x3+…+x2010×x2011+x2011×x2012的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网