题目内容
定义在R上的函数f(x)满足f(x+1)=-f(x),当0≤x≤1时,f(x)=-|x-
|+
,则f(
)-f(
)= .
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 99 |
| 2 |
考点:函数的值,函数的周期性
专题:函数的性质及应用
分析:根据对任意实数x满足条件f(x+1)=-f(x)这一条件得出f(x)的周期,进行解答即可.
解答:
解:∵f(x)是定义在R上的函数,且满足条件f(x+1)=-f(x);
∴f(x+2)=f[(x+1)+1]=-f(x+1)=-(-f(x))=f(x),
∴函数f(x)以2为周期的函数;
又∵0≤x≤1时,f(x)=-|x-
|+
,
∴f(
)=f(
-2)=f(
)=-|
-
|+
=
,
∴f(
)=f(
-50)=f(-
)=-f(-
+1)=-f(
)=-
;
∴f(
)-f(
)=
-(-
)=1.
故答案为:1.
∴f(x+2)=f[(x+1)+1]=-f(x+1)=-(-f(x))=f(x),
∴函数f(x)以2为周期的函数;
又∵0≤x≤1时,f(x)=-|x-
| 1 |
| 2 |
| 1 |
| 2 |
∴f(
| 5 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴f(
| 99 |
| 2 |
| 99 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴f(
| 5 |
| 2 |
| 99 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:1.
点评:本题考查了利用函数的周期性求函数值的问题,解题的关键是根据f(x+2)=-f(x)这一条件求出函数f(x)的周期,是基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
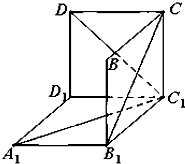 如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的.有如下结论:
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的.有如下结论: