题目内容
数列{an}的前n项和记为Sn,已知a1=1,an+1= Sn(n=1,2,3,…),证明:
Sn(n=1,2,3,…),证明:
(1) 数列 是等比数列;
是等比数列;
(2) Sn+1=4an.
证明:(1) ∵ an+1=Sn+1-Sn,an+1= Sn(n=1,2,3,…),∴ (n+2)Sn=n(Sn+1-Sn),
Sn(n=1,2,3,…),∴ (n+2)Sn=n(Sn+1-Sn),
整理得nSn+1=2(n+1)Sn,∴ ,
,
即 =2,∴ 数列
=2,∴ 数列 是等比数列.
是等比数列.
(2) 由(1)知: =4·
=4· (n≥2),于是Sn+1=4·(n+1)·
(n≥2),于是Sn+1=4·(n+1)· =4an(n≥2).又a2=3S1=3,∴ S2=a1+a2=1+3=4a1,
=4an(n≥2).又a2=3S1=3,∴ S2=a1+a2=1+3=4a1,
∴ 对一切n∈N*,都有Sn+1=4an.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
 =1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P.若
=1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P.若 ,则椭圆的离心率是________.
,则椭圆的离心率是________.
 =1上一点P到右焦点的距离是实轴两端点到右焦点距离的等差中项,则P点到左焦点的距离为________.
=1上一点P到右焦点的距离是实轴两端点到右焦点距离的等差中项,则P点到左焦点的距离为________.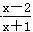 (a>1).
(a>1). =an+1-
=an+1-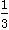 n2-n-
n2-n- ,n∈N*.
,n∈N*. +
+ +…+
+…+ <
< .
. 是⊙
是⊙ 的一条切线,切点为
的一条切线,切点为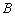 ,
, 都是⊙
都是⊙ .
. ;
; .
.