题目内容
已知f(x)＝ax＋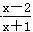
(a＞1)．
(1) 证明f(x)在(－1，＋∞)上为增函数；
(2) 用反证法证明方程f(x)＝0没有负数根．
证明：(1) 设－1＜x1＜x2，则x2－x1＞0，ax2－x1＞1，ax1＞0，x1＋1＞0，x2＋1＞0，从而f(x2)－f(x1)＝ax2－ax1＋
＝ax1(ax2－x1－1)＋
＞0，所以f(x)在(－1，＋∞)上为增函数．
(2) 设存在x0＜0(x0≠－1)使f(x0)＝0，则ax0＝－
.
由0＜ax0＜10＜－＜1，即
＜x0＜2，此与x0＜0矛盾，故x0不存在．
练习册系列答案
相关题目
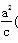(a为长半轴，c为半焦距)上．
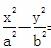＝1写出具有类似特性的性质，并加以证明．
Sn(n＝1，2，3，…)，证明：
是等比数列；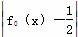
，fn(x)＝
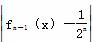，(n≥1，n≥N)，则方程f1(x)＝
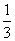有________个实数根，方程fn(x)＝
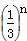有________个实数根．
，an＋1＝
，则a2，a3，a4，a5的值分别为________________，由此猜想an＝________．
)上有零点的函数是
（ ）
x