题目内容
已知
,
为非零向量,且
,
夹角为
,若向量
=
+
,则|
|= .
| a |
| b |
| a |
| b |
| π |
| 3 |
| p |
| ||
|
|
| ||
|
|
| p |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:将向量
=
+
平方,转化为
,
向量的数量积解答.
| p |
| ||
|
|
| ||
|
|
| a |
| b |
解答:
解:因为
,
为非零向量,且
,
夹角为
,向量
=
+
,
所以|
|2=(
+
)2=(
)2+(
)2+2
•
=1+1+2|
||
|cos
=1+1+1=3,
所以|
|=
;
故答案为:
.
| a |
| b |
| a |
| b |
| π |
| 3 |
| p |
| ||
|
|
| ||
|
|
所以|
| p |
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| π |
| 3 |
所以|
| p |
| 3 |
故答案为:
| 3 |
点评:本题考查了向量的数量积以及向量的模的运算.属于基础题.

练习册系列答案
相关题目
平面α的斜线l与它在这个平面上射影l′的方向向量分别为
=(1,0,1),
=(0,1,1),则斜线l与平面α所成的角为( )
| a |
| b |
| A、30° | B、45° |
| C、60° | D、90° |
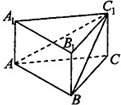 如图,在正三棱柱ABC-A1B1C1中,若AB=2,CC1=1,则点C到平面C1AB的距离等于
如图,在正三棱柱ABC-A1B1C1中,若AB=2,CC1=1,则点C到平面C1AB的距离等于