题目内容
已知函数y=4x+3×2x+3,当其值域为[1,7]时,求x的取值范围.
考点:指数型复合函数的性质及应用
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:令t=2x(t>0),可得y=t2+3t+3,由函数的值域为[1,7],得1≤t2+3t+3≤7,解出0<t≤1.再将t还原成2x,最后解关于x的不等式,即可得到实数x的取值范围.
解答:
解:令t=2x,可得y=4x+3•2x+3=t2+3t+3,(t>0)
∵函数的值域为[1,7],
∴解不等式1≤t2+3t+3≤7,可得
,即有
解此不等式组,由t>0,得0<t≤1,
∴0<2x≤1,即0<2x≤20,
因此,x的取值范围是(-∞,0].
∵函数的值域为[1,7],
∴解不等式1≤t2+3t+3≤7,可得
|
|
解此不等式组,由t>0,得0<t≤1,
∴0<2x≤1,即0<2x≤20,
因此,x的取值范围是(-∞,0].
点评:本题给出含有指数式的“类二次”函数,在已知值域的情况下求x的取值范围,着重考查了指数函数、二次函数的图象与性质和不等式的解法等知识,属于中档题.

练习册系列答案
相关题目
现将周长为24cm的圆改为矩形 (周长不变),则该矩形面积大于32cm2的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知实数x,y满足
,则z=2x+y的最小值是( )
|
| A、1 | B、2 | C、4 | D、8 |
函数y=sin(ωx+φ)的部分图象如图,则φ、ω可以取的一组值是( )
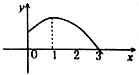

A、ω=
| ||||
B、ω=
| ||||
C、ω=
| ||||
D、ω=
|