题目内容
点P是椭圆
+y2=1上一点，且在第一象限内移动；O为原点，A（2，0），B（0，1），则四边形OAPB的面积的最大值是 ．
| x2 |
| 4 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：利用三角函数来解答这道题，椭圆方程
+y2=1上 里面的自变量x，y可以表示为 x=2cosa y=sina 本题中要求第一象限，这样就应该有0＜a＜π，
设P为（2cosa，sina）这样四边形OAPB的面积就可以表示为两个三角形OAP和OPB面积之和，
对于三角形OAP有面积S1=sina 对于三角形OBP有面积S2=cosa 这样四边形的面积S=S1+S2=sina+cosa也就相当于求解sina+cosa的最大值，
0＜a＜π，sina+cosa=
sin（a+
）这样其最大值就应该为
，并且当且仅当a=
时成立．
| x2 |
| 4 |
设P为（2cosa，sina）这样四边形OAPB的面积就可以表示为两个三角形OAP和OPB面积之和，
对于三角形OAP有面积S1=sina 对于三角形OBP有面积S2=cosa 这样四边形的面积S=S1+S2=sina+cosa也就相当于求解sina+cosa的最大值，
0＜a＜π，sina+cosa=
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
解答：
解：由于点P是椭圆程
+y2=1上上的在第一象限内的点，
设P为（2cosa，sina）即x=2cosa y=sina （0＜a＜π），
这样四边形OAPB的面积就可以表示为两个三角形OAP和OPB面积之和，
对于三角形OAP有面积S1=sina 对于三角形OBP有面积S2=cosa
∴四边形的面积S=S1+S2=sina+cosa
=
sin（a+
）
其最大值就应该为
，
并且当且仅当a=
时成立．所以，面积最大值
．
故答案为：
．
| x2 |
| 4 |
设P为（2cosa，sina）即x=2cosa y=sina （0＜a＜π），
这样四边形OAPB的面积就可以表示为两个三角形OAP和OPB面积之和，
对于三角形OAP有面积S1=sina 对于三角形OBP有面积S2=cosa
∴四边形的面积S=S1+S2=sina+cosa
=
| 2 |
| π |
| 4 |
其最大值就应该为
| 2 |
并且当且仅当a=
| π |
| 4 |
| 2 |
故答案为：
| 2 |
点评：本题主要考查了椭圆的简单性质，解答的关键在于利用椭圆的参数方程设出椭圆上一点的坐标，利用三角函数的有界性求最值．
练习册系列答案
相关题目
已知定义在R上的函数f（x）满足下列三个条件：
①对任意的x∈R，都有f（x+4）=f（x）；
②对任意的0≤x1＜x2≤2，都有f（x1）＜f（x2）；
③y=f（x+2）的图象关于y轴对称，
则下列结论中，正确的是（ ）
①对任意的x∈R，都有f（x+4）=f（x）；
②对任意的0≤x1＜x2≤2，都有f（x1）＜f（x2）；
③y=f（x+2）的图象关于y轴对称，
则下列结论中，正确的是（ ）
| A、f（7）＜f（4.5）＜f（6.5） |
| B、f（7）＜f（6.5）＜f（4.5） |
| C、f（4.5）＜f（6.5）＜f（7） |
| D、f（4.5）＜f（7）＜f（6.5） |
数列{
}的前n项和为Sn，且满足a1=1，an=an-1+n，（n≥2），则Sn等于（ ）
| an |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
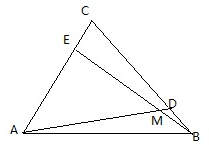如图，D、E分别为等边△ABC的边BC，AC上一点，BD=CE，∠CAD=45°，AD、BE交于M．