题目内容
在△ABC中，已知sinAcosB=sinC，那么△ABC一定是（ ）
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、正三角形 |
考点：三角形的形状判断
专题：解三角形
分析：利用诱导公式与两角和的正弦可得cosAsinB=0，又sinB＞0，可求得cosA=0，A=90°，从而可得答案．
解答：
解：在△ABC中，
∵sinAcosB=sinC=sin[π-（A+B）]=sin（A+B）=sinAcosB+cosAsinB，
∴cosAsinB=0，又sinB＞0，
∴cosA=0，A=90°
∴△ABC一定是直角三角形，
故选：A．
∵sinAcosB=sinC=sin[π-（A+B）]=sin（A+B）=sinAcosB+cosAsinB，
∴cosAsinB=0，又sinB＞0，
∴cosA=0，A=90°
∴△ABC一定是直角三角形，
故选：A．
点评：本题考查三角形的形状判断，着重考查诱导公式与两角和的正弦，考查转化思想．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
数列{
}的前n项和为Sn，且满足a1=1，an=an-1+n，（n≥2），则Sn等于（ ）
| an |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
用a，b表示两条不同的直线，γ表示平面，给出下列命题：
（1）若a∥γ，b∥γ，则a∥b
（2）若a∥b，b∥γ，则a∥γ
（3）若a⊥γ，b∥γ，则a⊥b
（4）若a⊥γ，b⊥γ，则a∥b
其中真命题的序号是（ ）
（1）若a∥γ，b∥γ，则a∥b
（2）若a∥b，b∥γ，则a∥γ
（3）若a⊥γ，b∥γ，则a⊥b
（4）若a⊥γ，b⊥γ，则a∥b
其中真命题的序号是（ ）
| A、（1）（4） |
| B、（2）（3） |
| C、（3）（4） |
| D、（1）（2） |
设全集为R，函数f（x）=
的定义域为M，函数f（x）=ln（x2-4x）的定义域为N，则M∩N=（ ）
| 4-x2 |
| A、[-2，0） |
| B、（-∞，-2] |
| C、（4，+∞） |
| D、（-∞，0]∪（4，+∞） |
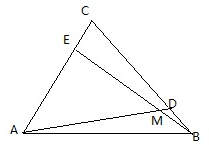如图，D、E分别为等边△ABC的边BC，AC上一点，BD=CE，∠CAD=45°，AD、BE交于M．