题目内容
已知函数f（x）=x3+ax2+bx+c在x=-2处取得极值，并且它的图象与直线y=-3x+3在点（1，0）处相切．
（1）求f（x）的解析式；
（2）求f（x）的单调区间；
（3）若关于x的方程f（x）=m有三个不同的是根，求m的值．
（1）求f（x）的解析式；
（2）求f（x）的单调区间；
（3）若关于x的方程f（x）=m有三个不同的是根，求m的值．
考点：利用导数研究曲线上某点切线方程,函数的零点与方程根的关系,利用导数研究函数的极值
专题：函数的性质及应用
分析：（1）求出函数的导数，利用已知条件得到方程组即可求出a、b、c，然后求f（x）的解析式；
（2）求出函数的导数，通过导函数的符号，判断f（x）的单调性，求出单调区间；
（3）若关于x的方程f（x）=m有三个不同的是根，求出函数的极值，然后求m的值．
（2）求出函数的导数，通过导函数的符号，判断f（x）的单调性，求出单调区间；
（3）若关于x的方程f（x）=m有三个不同的是根，求出函数的极值，然后求m的值．
解答：
解：（1）f′（x）=3x2+2ax+b，
∵函数f（x）在x=-2时取得极值，
∴f′（-2）=0，即12-4a+b=0①，
∵函数图象与直线y=-3x+3切于点P（1，0）．
∴f′（1）=-3，即 3+2a+b=-3②，
由f（1）=0，即 1+a+b+c=0③，
由①②③解得a=1，b=-8，c=6；
（2）由（1）知，f（x）=x3+x2-8x+6，f′（x）=3x2+2x-8=（3x-4）（x+2），
由f′（x）＞0得，x＜-2或x＞
，由f′（x）＜0得，-2＜x＜
，
所以f（x）在（-∞，-2）和（
，+∞）上递增，在（-2，
）上递减，
（3）由（2）知，当x=-2时f（x）取得极大值f（-2）=18，
当x=
时f（x）取得极小值f（
）=-
，
因为关于x的方程f（x）=m有三个不同实根，所以函数y=f（x）和y=m图象有三个交点，
所以-
＜m＜18，即为m的取值范围．
∵函数f（x）在x=-2时取得极值，
∴f′（-2）=0，即12-4a+b=0①，
∵函数图象与直线y=-3x+3切于点P（1，0）．
∴f′（1）=-3，即 3+2a+b=-3②，
由f（1）=0，即 1+a+b+c=0③，
由①②③解得a=1，b=-8，c=6；
（2）由（1）知，f（x）=x3+x2-8x+6，f′（x）=3x2+2x-8=（3x-4）（x+2），
由f′（x）＞0得，x＜-2或x＞
| 4 |
| 3 |
| 4 |
| 3 |
所以f（x）在（-∞，-2）和（
| 4 |
| 3 |
| 4 |
| 3 |
（3）由（2）知，当x=-2时f（x）取得极大值f（-2）=18，
当x=
| 4 |
| 3 |
| 4 |
| 3 |
| 62 |
| 27 |
因为关于x的方程f（x）=m有三个不同实根，所以函数y=f（x）和y=m图象有三个交点，
所以-
| 62 |
| 27 |
点评：本题考查函数的导数的应用，切线方程以及函数的极值，考查分析问题解决问题的能力．
练习册系列答案
优等生题库系列答案
相关题目
数列{
}的前n项和为Sn，且满足a1=1，an=an-1+n，（n≥2），则Sn等于（ ）
| an |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
设全集为R，函数f（x）=
的定义域为M，函数f（x）=ln（x2-4x）的定义域为N，则M∩N=（ ）
| 4-x2 |
| A、[-2，0） |
| B、（-∞，-2] |
| C、（4，+∞） |
| D、（-∞，0]∪（4，+∞） |
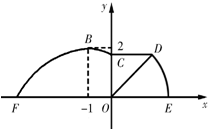如图，某市准备在道路EF的一侧修建一条运动比赛道，赛道的前一部分为曲线段FBC．该曲线段是函数y=Asin（ωx+
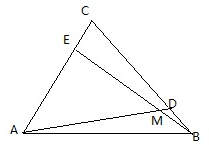如图，D、E分别为等边△ABC的边BC，AC上一点，BD=CE，∠CAD=45°，AD、BE交于M．
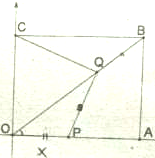如图，在矩形OABC中，O为原点，B点坐标为（8，6）．
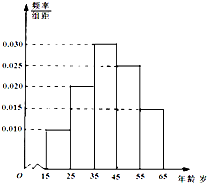为了了解我市各景点在大众中的熟知度，随机对15～65岁的人群抽样了n人，回答问题“我市有哪几个著名的旅游景点？”，统计结果见下表和各组人数的频率分布直方图（如图）：