题目内容
化简:
(1)asin0°+bcos90°+ctan180°;
(2)-p2cos180°+q2sin90°-2pqcos0°;
(3)a2cos2π-b2sin
+abcosπ-absin
;
(4)mtan0°+ncos
-psinπ-qcos
-rsin2π.
(1)asin0°+bcos90°+ctan180°;
(2)-p2cos180°+q2sin90°-2pqcos0°;
(3)a2cos2π-b2sin
| 3π |
| 2 |
| π |
| 2 |
(4)mtan0°+ncos
| π |
| 2 |
| 3π |
| 2 |
考点:任意角的三角函数的定义
专题:三角函数的求值
分析:由条件利用特殊角的三角函数的值,求得各个式子的值.
解答:
解:(1)asin0°+bcos90°+ctan180°=a•0+b•0+c•0=0;
(2)-p2cos180°+q2sin90°-2pqcos0°=p2+q2-2pq=(p-q)2;
(3)a2cos2π-b2sin
+abcosπ-absin
=a2+b2--ab-ab=(a-b)2;
(4)mtan0°+ncos
-psinπ-qcos
-rsin2π=m•0+n•0-p•0-q•0-r•0=0
(2)-p2cos180°+q2sin90°-2pqcos0°=p2+q2-2pq=(p-q)2;
(3)a2cos2π-b2sin
| 3π |
| 2 |
| π |
| 2 |
(4)mtan0°+ncos
| π |
| 2 |
| 3π |
| 2 |
点评:本题主要考查特殊角的三角函数的值,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
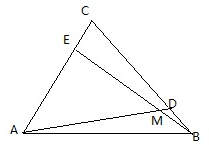 如图,D、E分别为等边△ABC的边BC,AC上一点,BD=CE,∠CAD=45°,AD、BE交于M.
如图,D、E分别为等边△ABC的边BC,AC上一点,BD=CE,∠CAD=45°,AD、BE交于M.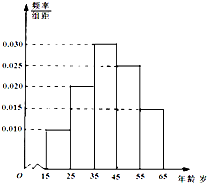 为了了解我市各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“我市有哪几个著名的旅游景点?”,统计结果见下表和各组人数的频率分布直方图(如图):
为了了解我市各景点在大众中的熟知度,随机对15~65岁的人群抽样了n人,回答问题“我市有哪几个著名的旅游景点?”,统计结果见下表和各组人数的频率分布直方图(如图):