题目内容
已知a，b，c是钝角△ABC中∠A，∠B，∠C的对边，∠C为钝角，△ABC的面积是5
，a=4，b=5，则c= ．
| 3 |
考点：正弦定理,余弦定理
专题：解三角形
分析：利用三角形面积公式列出关系式，把a，b，已知面积代入求出sinC的值，确定出C的度数，利用余弦定理即可求出c的值．
解答：
解：∵a=4，b=5，△ABC面积S=
absinC=5
，
∴sinC=
，
∵C为钝角，
∴C=120°，
由余弦定理得：c2=a2+b2-2abcosC=16+25-20=21，
则c=
，
故答案为：
| 1 |
| 2 |
| 3 |
∴sinC=
| ||
| 2 |
∵C为钝角，
∴C=120°，
由余弦定理得：c2=a2+b2-2abcosC=16+25-20=21，
则c=
| 21 |
故答案为：
| 21 |
点评：此题考查了余弦定理，以及三角形面积公式，熟练掌握定理及公式是解本题的关键．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
数列{
}的前n项和为Sn，且满足a1=1，an=an-1+n，（n≥2），则Sn等于（ ）
| an |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
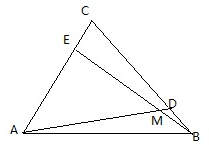如图，D、E分别为等边△ABC的边BC，AC上一点，BD=CE，∠CAD=45°，AD、BE交于M．
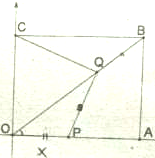如图，在矩形OABC中，O为原点，B点坐标为（8，6）．
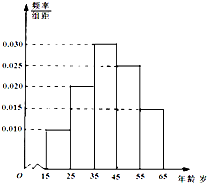为了了解我市各景点在大众中的熟知度，随机对15～65岁的人群抽样了n人，回答问题“我市有哪几个著名的旅游景点？”，统计结果见下表和各组人数的频率分布直方图（如图）：