题目内容
设函数f(x)=|x-1|+|x+1|.
(Ⅰ)解不等式f(x)≥3
(Ⅱ)如果?x∈R,都有f(x)≥a恒成立,求a的取值范围.
(Ⅰ)解不等式f(x)≥3
(Ⅱ)如果?x∈R,都有f(x)≥a恒成立,求a的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)通过对x取值范围的分类讨论,去掉绝对值不等式中的绝对值符号,转化为一次不等式,分别解之,最后取并集即可;
(Ⅱ)利用绝对值不等式的几何意义易求f(x)min=2,从而可求a的取值范围.
(Ⅱ)利用绝对值不等式的几何意义易求f(x)min=2,从而可求a的取值范围.
解答:
解:(Ⅰ)∵f(x)=|x-1|+|x+1|=
,
∴f(x)≥3?
,
解得:x≤-
或x≥
,
∴不等式f(x)≥3的解集为{x|x≤-
或x≥
};
(Ⅱ)?x∈R,都有f(x)≥a恒成立?a≤f(x)min,
∵f(x)=|x-1|+|x+1|≥|(x-1)-(x+1)|=2,
∴f(x)min=2,
∴a≤2,即a的取值范围为(-∞,2].
|
∴f(x)≥3?
|
解得:x≤-
| 3 |
| 2 |
| 3 |
| 2 |
∴不等式f(x)≥3的解集为{x|x≤-
| 3 |
| 2 |
| 3 |
| 2 |
(Ⅱ)?x∈R,都有f(x)≥a恒成立?a≤f(x)min,
∵f(x)=|x-1|+|x+1|≥|(x-1)-(x+1)|=2,
∴f(x)min=2,
∴a≤2,即a的取值范围为(-∞,2].
点评:本题考查绝对值不等式的解法,突出考查等价转化思想与方程思想、分类讨论思想的综合应用,属于中档题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
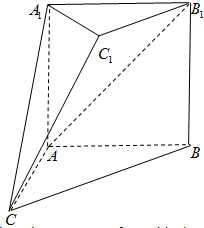 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,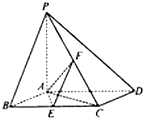 如图,已知四棱锥P-ABCD,底面ABCD是边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD是边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.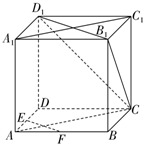 如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AD、AB的中点.求证:EF∥平面CB1D1.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AD、AB的中点.求证:EF∥平面CB1D1.