题目内容
(文科)已知函数f(x)=
,下面结论中,所有正确结论的序号是 .
①f(f(x))=1
②函数f(x)是偶函数
③任取一个不为0的有理数T,f(x+T)=f(x)对x∈R恒成立
④存在三个点A(x1,f(x1)),B(x2,f(x2)),C(x3,f(x3))使得△ABC为等边三角形.
|
①f(f(x))=1
②函数f(x)是偶函数
③任取一个不为0的有理数T,f(x+T)=f(x)对x∈R恒成立
④存在三个点A(x1,f(x1)),B(x2,f(x2)),C(x3,f(x3))使得△ABC为等边三角形.
考点:命题的真假判断与应用
专题:简易逻辑
分析:根据函数的对应法则,可得不管x是有理数还是无理数,均有f(f(x))=1;
根据函数图象的特点,可得f(x)是偶函数;
根据函数的表达式,结合有理数和无理数的性质,得③正确;
取x1=-
,x2=0,x3=
,可得A(-
,0)、B(0,1)、C(
,0)三点恰好构成等边三角形,得④正确.
根据函数图象的特点,可得f(x)是偶函数;
根据函数的表达式,结合有理数和无理数的性质,得③正确;
取x1=-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
解答:
解:函数f(x)=
,
①当x∈Q时,f(f(x))=f(1)=1.
当x∈∁RQ时,f(f(x))=f(0)=1.①正确;
②∵f(x)=
的图象关于y轴对称,函数f(x)是偶函数.②正确;
③∵有理数与有理数的和为有理数,有理数与无理数的和为无理数,
∴任取一个不为0的有理数T,f(x+T)=f(x)对x∈R恒成立.③正确;
④取x1=-
,x2=0,x3=
,可得A(-
,0)、B(0,1)、C(
,0)三点恰好构成等边三角形.④正确.
故答案为:①②③④.
|
①当x∈Q时,f(f(x))=f(1)=1.
当x∈∁RQ时,f(f(x))=f(0)=1.①正确;
②∵f(x)=
|
③∵有理数与有理数的和为有理数,有理数与无理数的和为无理数,
∴任取一个不为0的有理数T,f(x+T)=f(x)对x∈R恒成立.③正确;
④取x1=-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
故答案为:①②③④.
点评:本题给出特殊函数表达式,求函数的值并讨论它的奇偶性,着重考查了有理数、无理数的性质和函数的奇偶性等知识,属于中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
已知数列{an}的前n项和为Sn=1-5+9-13+17-21+…+(-1)n+1(4n-3),则S15+S22-S31的值是( )
| A、-76 | B、76 | C、46 | D、13 |
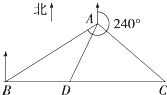 海上一观测站测得方位角240°的方向上有一艘停止待修的商船,在商船的正东方有一艘海盗船正向它靠近,速度为每小时90海里.此时海盗船距观测站10
海上一观测站测得方位角240°的方向上有一艘停止待修的商船,在商船的正东方有一艘海盗船正向它靠近,速度为每小时90海里.此时海盗船距观测站10