题目内容
18.已知函数f(x)=$\left\{\begin{array}{l}{{3}^{x}-\frac{1}{{3}^{x}},x≥0}\\{0,x<0}\end{array}\right.$(1)若f(x)=2,求x的值;
(2)若3x•f(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
分析 (1)f(x)=2即3x-$\frac{1}{{3}^{x}}$=2,先解3x,再解x值,注意3x>0;
(2)不等式3t•f(2t)+mf(t)≥0恒成立,通过整理变形转化为32t+1+m≥0恒成立,分离参数m后转化为求函数最值问题解决
解答 解:(1)f(x)=2即3x-$\frac{1}{{3}^{x}}$=2,得32x-2×3x-1=0,∴3x=1±$\sqrt{2}$,
又3x>0,∴3x=1+$\sqrt{2}$,
∴x=log3(1+$\sqrt{2}$).
(2)∵3t•f(2t)+mf(t)≥0,
∴3t(32t-3-2t)+m(3t-3-t)≥0,
∵t∈[1,2],
∴32t+1+m≥0恒成立,即m≥-(32t+1)恒成立,
问题等价于m大于等于-(32t+1)的最大值-10,
∴m≥-10,
因此m的取值范围为[-10,+∞).
点评 本题考查函数恒成立问题及指数方程的求解,考查学生的分析问题解决问题的能力,恒成立问题往往转化为求函数最值问题解决,或分离参数后再求函数最值.

练习册系列答案
相关题目
8.经过点M(2,2)且在两轴上截距相等的直线是( )
| A. | x+y=4 | B. | x+y=2 | C. | x=2或y=2 | D. | x+y=4或x=y |
6.若关于x的方程9x+(4+a)3x+4=0有解,则实数a的取值范围是( )
| A. | (-∞,-8] | B. | (-∞,-8]∪[0,+∞) | C. | (-∞,-4) | D. | [-8,4) |
13.设max{p,q}表示p,q两者中的较大者,若函数f(x)=max{1-x,2x},则满足f(x)>4的x的集合为( )
| A. | (-∞,-3)∪(2,+∞) | B. | (-∞,-3) | C. | (-3,2) | D. | (2,+∞) |
3.已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则(∁UA)∪B为( )
| A. | {1,2,4} | B. | {2,3,4} | C. | {0,2,4} | D. | {0,2,3,4} |
7.用0,1,2,3,4,5 组成没有重复的三位数,其中偶数共有( )
| A. | 24个 | B. | 30个 | C. | 52个 | D. | 60个 |
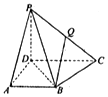 在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是直角梯形,AD⊥DC,AB∥DC,DC=2AB,设Q为棱PC上一点,$\overrightarrow{PQ}$=λ$\overrightarrow{PC}$
在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是直角梯形,AD⊥DC,AB∥DC,DC=2AB,设Q为棱PC上一点,$\overrightarrow{PQ}$=λ$\overrightarrow{PC}$