题目内容
7.用0,1,2,3,4,5 组成没有重复的三位数,其中偶数共有( )| A. | 24个 | B. | 30个 | C. | 52个 | D. | 60个 |
分析 根据题意,按照个位数字的不同,分2种情况讨论:①、个位数字为0,在1、2、3、4、5 这5个数中任取2个,安排在十位、百位,由排列数公式可得其情况数目,②、个位数字为2或4,分析百位、十位数字的取法数目,由乘法原理可得此时的情况数目,进而由分类计数原理计算可得答案.
解答 解:根据题意,要求组成三位偶数,其个位数字为0、2、4,则分2种情况讨论:
①、个位数字为0,在1、2、3、4、5 这5个数中任取2个,安排在十位、百位,有A52=20种情况,
②、个位数字为2或4,有2种情况,
由于0不能在百位,百位数字在其余4个数字中任取1个,有4种情况,
十位数字在剩下的4个数字中任取1个,有4种情况,
则有2×4×4=32种情况,
则有20+32=52种情况,即其中偶数有52个;
故选:C.
点评 本题考查排列、组合的应用,需要注意特殊数位上的数,比如,最高位不能是0,偶数的个位必须是,0、2、4这些数,再根据乘法原理解答即可

练习册系列答案
相关题目
15.张君四年前买了50000元的某种基金,收益情况是前两年每年递减20%,后两年每年递增20%,则现在的价值与原来价值比较,变化的情况是( )
| A. | 减少7.84% | B. | 增加7.84% | C. | 减少9.5% | D. | 增加 |
2.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
| A. | 若m⊥α,m∥n,n∥β,则 α⊥β | B. | 若α∥β,m?α,n?β,则 m∥n | ||
| C. | 若m⊥n,m?α,n?β,则α⊥β | D. | 若α⊥β,m?α,n?β,则m⊥n |
12.已知球O是的棱长为1的正方体ABCD-A1B1C1D1的内切球,则平面ACD1截球O的截面面积为( )
| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
19.如图所示,程序框图输出的结果是( )


| A. | 55 | B. | 89 | C. | 144 | D. | 233 |
16.命题“?x0∈R,$\frac{2}{{x}_{0}}$+lnx0≤0”的否定是( )
| A. | ?x∈R,$\frac{2}{x}$+lnx>0 | B. | ?x∈R,$\frac{2}{x}$+lnx≥0 | ||
| C. | ?x0∈R,$\frac{2}{{x}_{0}}$+lnx0<0 | D. | ?x0∈R,$\frac{2}{{x}_{0}}$+lnx0>0 |
17.已知简单组合体的三视图如图所示,则此简单组合体的体积为( )
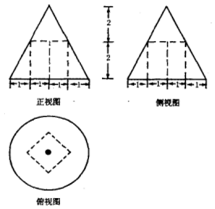

| A. | $\frac{10π}{3}-4$ | B. | $\frac{10π}{3}-8$ | C. | $\frac{16π}{3}-4$ | D. | $\frac{16π}{3}-8$ |