题目内容
13.已知函数f(x)=xlnx.(1)求函数y=f(x)的单调区间;
(2)证明:当x>0时,$xlnx>\frac{x}{e^x}-\frac{2}{e}$..
分析 (1)先求出函数的导数,从而求出函数的单调区间;
(2)令g(x)=$\frac{x}{{e}^{x}}$-$\frac{2}{x}$,(x>0),根据函数的单调性求出g(x)的最大值,从而证出结论即可.
解答 解:(1)函数的定义域为(0,+∞).
因为f′(x)=lnx+1,
令f′(x)=0,即x=$\frac{1}{e}$,
当0<x<$\frac{1}{e}$时,f′(x)<0;当x>$\frac{1}{e}$时,f′(x)>0,
所以f(x)的单调递减区间为(0,$\frac{1}{e}$),单调递增区间为($\frac{1}{e}$,+∞).
(2)证明:由(1)得:f(x)=xlnx在最小值是-$\frac{1}{e}$,
当且仅当x=$\frac{1}{e}$时取得,
令g(x)=$\frac{x}{{e}^{x}}$-$\frac{2}{x}$,(x>0),则g′(x)=$\frac{1-x}{{e}^{x}}$,x>0,
当x>1时,g′(x)<0,当0<x<1时,g′(x)>0,
故g(x)在最大值是g(1)=-$\frac{1}{e}$,
当且仅当x=1时取得,
故原不等式成立.
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及不等式的证明,是一道中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
3.已知z=$\frac{4-3i}{3+4i}$+2(i为虚数单位),则z在复平面内所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.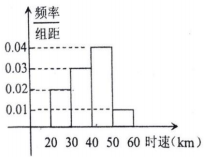 太原市某时段100辆汽车通过祥云桥时,时速的频率分布直方图如图所示,则时速在[30,40]的汽车约有( )
太原市某时段100辆汽车通过祥云桥时,时速的频率分布直方图如图所示,则时速在[30,40]的汽车约有( )
 太原市某时段100辆汽车通过祥云桥时,时速的频率分布直方图如图所示,则时速在[30,40]的汽车约有( )
太原市某时段100辆汽车通过祥云桥时,时速的频率分布直方图如图所示,则时速在[30,40]的汽车约有( )| A. | 30辆 | B. | 35辆 | C. | 40辆 | D. | 50辆 |
18.函数y=$\frac{1}{{\sqrt{{{log}_{0.6}}(4x-3)}}}$的定义域为( )
| A. | $(\frac{3}{4},+∞)$ | B. | $(\frac{3}{4},1)$ | C. | (1+∞) | D. | $(\frac{3}{4},1)∪(1+∞)$ |
5.设f(x)=ex-x-2,则函数f(x)的零点所在区间是( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |