题目内容
设P、Q为两个非空实数集合,定义集合P+Q={x|x=a+b,a∈P,b∈Q},若P={0,2},Q={1,2,3},则P+Q= .(用例举法表示)
考点:元素与集合关系的判断
专题:计算题,集合
分析:由题意可得x=0+1=1,x=0+2=2,x=0+3=3,x=2+1=3,x=2+2=4,x=2+3=5;从而得到集合.
解答:
解:∵P+Q={x|x=a+b,a∈P,b∈Q},且P={0,2},Q={1,2,3},
∴x=0+1=1,x=0+2=2,x=0+3=3,
x=2+1=3,x=2+2=4,x=2+3=5;
故P+Q={1,2,3,4,5},
故答案为:{1,2,3,4,5}.
∴x=0+1=1,x=0+2=2,x=0+3=3,
x=2+1=3,x=2+2=4,x=2+3=5;
故P+Q={1,2,3,4,5},
故答案为:{1,2,3,4,5}.
点评:本题考查了元素与集合的关系及元素的特征,属于基础题.

练习册系列答案
相关题目
已知a=log23,b=log
5,c=(
)0.3则( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、a<b<c |
| B、a<c<b |
| C、b<c<a |
| D、b<a<c |
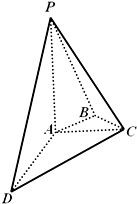 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1.