题目内容
已知
=(bsin
,acos
),
=(cos
,-cos
),f(x)=
•
+a,其中a,b,x∈R.且满足f(
)=2,f′(0)=
.
(Ⅰ)求a,b的值;
(Ⅱ)若关于x的方程f(x)-log
k=0在区间[0,π]上总有实数解,求实数k的取值范围.
| m |
| x |
| 2 |
| x |
| 2 |
| n |
| x |
| 2 |
| x |
| 2 |
| m |
| n |
| π |
| 3 |
| 3 |
(Ⅰ)求a,b的值;
(Ⅱ)若关于x的方程f(x)-log
| 1 |
| 3 |
考点:平面向量数量积的运算,根的存在性及根的个数判断
专题:平面向量及应用
分析:(I)利用数量积运算和倍角公式、导数的运算法则即可得出;
(II)利用正弦函数的单调性可得函数f(x)的值域,再利用对数函数的单调性即可得出.
(II)利用正弦函数的单调性可得函数f(x)的值域,再利用对数函数的单调性即可得出.
解答:
解:(I)由题意知f(x)=
•
+a=bsin
cos
-acos2
+a=
(1-cosx)+
sinx,
由f(
)=2得,a+
b=8,(*)
∵f′(x)=
sinx+
cosx,又f′(0)=
,
∴b=2
,
代入(*)解得a=2.
(Ⅱ)由(Ⅰ)得f(x)=1-cosx+
sinx=2sin(x-
)+1,
∵x∈[0,π],-
≤x-
≤
,
∴-1≤2sin(x-
)≤2,f(x)∈[0,3].
又∵f(x)-log
k=0有解,即f(x)=-log3k有解,
∴-3≤log3k≤0,解得
≤k≤1,
∴实数k的取值范围为[
,1].
| m |
| n |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| a |
| 2 |
| b |
| 2 |
由f(
| π |
| 3 |
| 3 |
∵f′(x)=
| a |
| 2 |
| b |
| 2 |
| 3 |
∴b=2
| 3 |
代入(*)解得a=2.
(Ⅱ)由(Ⅰ)得f(x)=1-cosx+
| 3 |
| π |
| 6 |
∵x∈[0,π],-
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴-1≤2sin(x-
| π |
| 6 |
又∵f(x)-log
| 1 |
| 3 |
∴-3≤log3k≤0,解得
| 1 |
| 27 |
∴实数k的取值范围为[
| 1 |
| 27 |
点评:本题考查了数量积运算和倍角公式、导数的运算法则、正弦函数的单调性、对数函数的单调性等基础知识与基本技能方法,考查了计算能力,属于中档题.

练习册系列答案
相关题目
下列说法中,正确的是( )
| A、命题“若am2<bm2,则a<b”的逆命题是真命题 |
| B、命题“p或q”为真命题,则命题“p”和命题“q”均为真命题 |
| C、命题“?x∈R,x2-x>0”的否定是:“?x∈R,x2-x≤0” |
| D、已知x∈R,则“x>1”是“x>2”的充分不必要条件 |
若x,y满足约束条件
,则z=2x+3y的最小值为( )
|
| A、7 | B、10 | C、16 | D、19 |
z=x-y在
的线性约束条件下,取得最大值的可行解为( )
|
| A、(0,1) | ||||
| B、(-1,-1) | ||||
| C、(1,0) | ||||
D、(
|
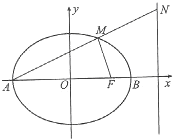 如图,已知椭圆E的中心为O,长轴的两个端点为A,B,右焦点为F,且
如图,已知椭圆E的中心为O,长轴的两个端点为A,B,右焦点为F,且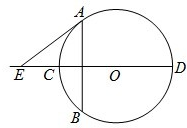 如图,AB是圆O的弦,CD是AB的垂直平分线,切线AE与DC的延长线相交于E.若AB=24,AE=20,则圆O的半径R=
如图,AB是圆O的弦,CD是AB的垂直平分线,切线AE与DC的延长线相交于E.若AB=24,AE=20,则圆O的半径R=