题目内容
7. 如图,已知四边形ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点,
如图,已知四边形ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点,(1)求证:MN∥平面PAD
(2)若PA=AD,求证:MN⊥平面PCD.
分析 (1)推导出AB⊥AD,PA⊥AB,从而AB⊥平面PAD,取CD中点O,连结MO、NO,推导出平面MON∥平面PAD,从而AB⊥平面MON,由此能证明MN⊥AB.
(2)由(1)得MN⊥CD,取PD中点G,连结AG、NG,则四边形AMNG是平行四边形,推导出MN⊥PD,由此能证明MN⊥平面PCD.
解答 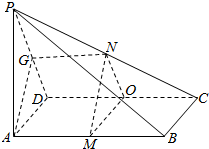 明:(1)∵四边形ABCD是矩形,∴AB⊥AD,
明:(1)∵四边形ABCD是矩形,∴AB⊥AD,
∵PA⊥平面ABC,∴PA⊥AB,
∵PA∩AD=A,∴AB⊥平面PAD,
取CD中点O,连结MO、NO,
∵M,N分别是AB,PC的中点,∴MO∥AD,NO∥PD,
∵MO∩NO=O,AD∩PD=D,
MO,NO?平面MON,AD、PD?平面PAD,
∴平面MON∥平面PAD,
∴AB⊥平面MON,∴MN⊥AB.
(2)∵MN⊥AB,AB∥CD,∴MN⊥CD,
取PD中点G,连结AG、NG,则NG∥DC,NG=$\frac{1}{2}$DC,∵AM∥DC,AM=$\frac{1}{2}DC$,
∴四边形AMNG是平行四边形,MN∥AG,
∵PA=AD,G是PD中点,∴AG⊥PD,∴MN⊥PD,
∵PD∩CD=D,∴MN⊥平面PCD.
点评 本题考查异面直线垂直\线面垂直的判定、空间思维能力.属于中档题.

练习册系列答案
相关题目
18. 已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为${F_1}{、_{_1}}{F_2}$,点B是双曲线的右顶点,A是其虚轴的端点,如图所示.若${S_{△AB{F_2}}}=\frac{1}{4}{S_{△AOB}}$,则双曲线的两条渐近线的夹角(锐角或直角)的正切值为( )
已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为${F_1}{、_{_1}}{F_2}$,点B是双曲线的右顶点,A是其虚轴的端点,如图所示.若${S_{△AB{F_2}}}=\frac{1}{4}{S_{△AOB}}$,则双曲线的两条渐近线的夹角(锐角或直角)的正切值为( )
 已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为${F_1}{、_{_1}}{F_2}$,点B是双曲线的右顶点,A是其虚轴的端点,如图所示.若${S_{△AB{F_2}}}=\frac{1}{4}{S_{△AOB}}$,则双曲线的两条渐近线的夹角(锐角或直角)的正切值为( )
已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为${F_1}{、_{_1}}{F_2}$,点B是双曲线的右顶点,A是其虚轴的端点,如图所示.若${S_{△AB{F_2}}}=\frac{1}{4}{S_{△AOB}}$,则双曲线的两条渐近线的夹角(锐角或直角)的正切值为( )| A. | $\frac{5}{4}$ | B. | $\frac{24}{7}$ | C. | $-\frac{21}{24}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
2.已知函数$f(x)=lnx-x+\frac{1}{x}$,若a=f(3),b=f(π),c=f(5),则( )
| A. | c<b<a | B. | c<a<b | C. | b<c<a | D. | a<c<b |
 在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=$2\sqrt{2}$a,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.G为PE的中点.
在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=$2\sqrt{2}$a,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.G为PE的中点.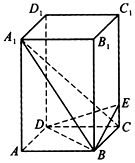 如图,在四棱柱ABCD-A1B1C1D1中,侧棱CC1垂直于底面,E为侧棱CC1上的点,底面ABCD为正方形,底面边长|AB|=2,侧棱|BB1|=4,|CE|=1
如图,在四棱柱ABCD-A1B1C1D1中,侧棱CC1垂直于底面,E为侧棱CC1上的点,底面ABCD为正方形,底面边长|AB|=2,侧棱|BB1|=4,|CE|=1