题目内容
已知函数f(x)=x3+x,x∈R
(1)不必证明,直接写出f(x)在R上的单调性;
(2)证明:f(x)是奇函数;
(3)解关于t的不等式f(1-t)+f(2t-3)>0.
(1)不必证明,直接写出f(x)在R上的单调性;
(2)证明:f(x)是奇函数;
(3)解关于t的不等式f(1-t)+f(2t-3)>0.
考点:利用导数研究函数的单调性,函数单调性的性质,函数奇偶性的判断
专题:导数的综合应用
分析:(1)求函数的导数,利用函数单调性和导数之间的关系即可写出f(x)在R上的单调性;
(2)根据函数奇偶性的定义即可证明:f(x)是奇函数;
(3)利用函数的奇偶性和单调性将不等式f(1-t)+f(2t-3)>0进行转化即可得到结论.
(2)根据函数奇偶性的定义即可证明:f(x)是奇函数;
(3)利用函数的奇偶性和单调性将不等式f(1-t)+f(2t-3)>0进行转化即可得到结论.
解答:
解:(1)函数的导数f′(x)=3x2+1>0,
则函数f(x)单调递增,即f(x)在R上的单调递增;
(2)由f(-x)=-x3-x=-(x3+x)=-f(x),则f(x)是奇函数;
(3)不等式f(1-t)+f(2t-3)>0等价为f(2t-3)>-f(1-t)=f(t-1),
∵f(x)在R上的单调递增,
∴2t-3>t-1,
即t>2.
则函数f(x)单调递增,即f(x)在R上的单调递增;
(2)由f(-x)=-x3-x=-(x3+x)=-f(x),则f(x)是奇函数;
(3)不等式f(1-t)+f(2t-3)>0等价为f(2t-3)>-f(1-t)=f(t-1),
∵f(x)在R上的单调递增,
∴2t-3>t-1,
即t>2.
点评:本题主要考查函数单调性,奇偶性以及不等式的解法,利用函数奇偶性和单调性的性质是解决不等式的关键.

练习册系列答案
相关题目
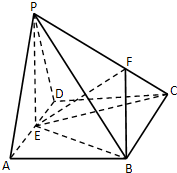 如图,四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,AB=2,PE=
如图,四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,AB=2,PE= 已知函数f(x)=2cosxsin(x+
已知函数f(x)=2cosxsin(x+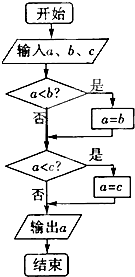 阅读如图的算法流程图:若a=sin60°,b=cos60°,c=tan60°,则输出的应该是
阅读如图的算法流程图:若a=sin60°,b=cos60°,c=tan60°,则输出的应该是