题目内容
若以连续掷两次骰子分别得到的点数m,n作为点P的坐标,求点P落在圆x2+y2=16外部的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:计算题,概率与统计
分析:本题是一个古典概型,试验发生包含的事件是连续掷两次骰子分别得到的点数m、n作为点P的坐标,共有6×6种结果,而满足条件的事件是点P落在圆x2+y2=16内,列举出落在圆内的情况共有8种结果,求比值,即可得到点P落在圆x2+y2=16外部的概率.
解答:
解:由题意知,本题是一个古典概型,
试验发生包含的事件是连续掷两次骰子分别得到的点数m、n作为点P的坐标,共有6×6=36种结果,
而满足条件的事件是点P落在圆x2+y2=16内,列举出落在圆内的情况:(1,1)(1,2)(1,3)
(2,1)(2,2)(2,3)(3,1)(3,2),共有8种结果,
根据古典概型概率公式得到点P落在该圆外部的概率为
=
.
故选:C.
试验发生包含的事件是连续掷两次骰子分别得到的点数m、n作为点P的坐标,共有6×6=36种结果,
而满足条件的事件是点P落在圆x2+y2=16内,列举出落在圆内的情况:(1,1)(1,2)(1,3)
(2,1)(2,2)(2,3)(3,1)(3,2),共有8种结果,
根据古典概型概率公式得到点P落在该圆外部的概率为
| 36-8 |
| 36 |
| 7 |
| 9 |
故选:C.
点评:本题主要考查等可能事件的概率,分别计算出事件总个数及满足条件的事件个数是解答的关键.

练习册系列答案
相关题目
正方体A1B1C1D1-ABCD中,AB与B1D1成的角是( )
| A、30° | B、45° |
| C、60° | D、90° |
抛掷红、黄两颗骰子,当红色骰子的点数为4或6时,两颗骰子的点数之积大于20的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
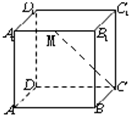 如图,在正方体ABCD-A1B1C1D1中,M为A1B1的中点,则MC与平面ABCD所成角的正弦值等于( )
如图,在正方体ABCD-A1B1C1D1中,M为A1B1的中点,则MC与平面ABCD所成角的正弦值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设火箭发射成功的概率为0.99,若发射10次,其中失败的次数为X,则E(X)等于( )
| A、0.01 | ||
| B、9.9 | ||
| C、0.1 | ||
D、C
|
在约束条件
下,目标函数z=ax+by(a>0,b>0)的最大值为
,则ab的最大值为( )
|
| 1 |
| 4 |
| A、32 | ||
| B、64 | ||
C、
| ||
D、
|
若tanα=
,则
的值为( )
| 1 |
| 3 |
| sinα+cosα |
| sinα-cosα |
| A、1 | B、-1 | C、2 | D、-2 |
已知三棱锥的三视图如图所示,其中侧视图为直角三角形,俯视图为等腰直角三角形,则此三棱锥的体积等于( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|