题目内容
4．x（x-3）＜0是|x-1|＜2成立的充分不必要条件．分析 分别解出不等式即可判断出关系．
解答 解：x（x-3）＜0，解得0＜x＜3．
由|x-1|＜2，解得：-1＜x＜3．
∴x（x-3）＜0是|x-1|＜2成立的充分不必要条件．
故答案为：充分不必要．
点评 本题考查了不等式的解法、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
15．
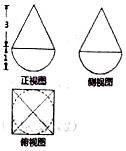一个由半球和四棱锥组成的几何体，其三视图如图所示，则该几何体的体积为（ ）
一个由半球和四棱锥组成的几何体，其三视图如图所示，则该几何体的体积为（ ）| A． | $4+\frac{2π}{3}$ | B． | $4+\frac{{\sqrt{2}π}}{6}$ | C． | $2+\frac{2π}{3}$ | D． | $2+\frac{{\sqrt{2}π}}{6}$ |
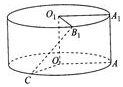将边长为1的正方形AA1O1O（及其内部）绕OO1旋转一周形成圆柱，如图，∠AOC=120°，∠A1O1B1=60°，其中B1与C在平面AA1O1O的同侧，则异面直线B1C与AA1所成角的大小是45°．
14．已知复数z满足（$\sqrt{3}$+3i）z=3i，则z等于（ ）
| A． | $\frac{3}{2}$-$\frac{\sqrt{3}}{2}$i | B． | $\frac{3}{4}$-$\frac{\sqrt{3}}{4}$i | C． | $\frac{3}{2}$+$\frac{\sqrt{3}}{2}$i | D． | $\frac{3}{4}$+$\frac{\sqrt{3}}{4}$i |