题目内容
12．
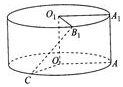将边长为1的正方形AA1O1O（及其内部）绕OO1旋转一周形成圆柱，如图，∠AOC=120°，∠A1O1B1=60°，其中B1与C在平面AA1O1O的同侧，则异面直线B1C与AA1所成角的大小是45°．
分析 如图所示，建立空间直角坐标系．利用向量夹角公式即可得出．
解答 解：如图所示，建立空间直角坐标系．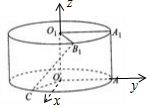
O（0，0，0），A（0，1，0），A1（0，1，1），C$（\frac{\sqrt{3}}{2}，-\frac{1}{2}，0）$，
B1$（\frac{\sqrt{3}}{2}，\frac{1}{2}，1）$．
∴$\overrightarrow{A{A}_{1}}$=（0，0，1），$\overrightarrow{C{B}_{1}}$=（0，1，1）．
设异面直线B1C与AA1所成角为θ．
∴cosθ=$\frac{1}{1×\sqrt{2}}$=$\frac{\sqrt{2}}{2}$．
故答案为：45°．
点评 本题考查了空间角、向量夹角公式、数量积运算性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
17．定义在R上的偶函数f（x）满足f（2-x）=f（x），且在[-3，-2]上是减函数，α，β是钝角三角形的两个锐角，则f（sinα）与f（cosβ）的大小关系是（ ）
| A． | f（sinα）＞f（cosβ） | B． | f（sinα）＜f（cosβ） | C． | f（sinα）=f（cosβ） | D． | f（sinα）≥f（cosβ） |
1．设全集U=R，集合A={3，4，5，6，7}，B={x|3＜x＜7}，则A∩（∁UB）=（ ）
| A． | {3，5，7} | B． | {3，7} | C． | {4，5，6} | D． | {5} |
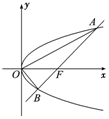如图，过抛物线y2=2px（p＞0）的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A，B两点．