Question

圆x²+y²+2y-3=0被直线x+y-k=0分成两段圆弧，且较短弧长与较长弧长之比为1：3，则k=（　　）

• A、

  2

  -1或-

  2

  -1
• B、1或-3
• C、1或-

  2

• D、

  2

Answer 1

考点：直线与圆相交的性质

专题：直线与圆

分析：设直线和圆相交于AB，则根据较短弧长与较长弧长之比为1：3得到对应三角形为直角三角形，利用点与直线的距离建立条件关系即可．

解答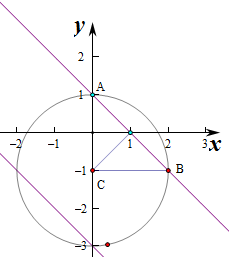： 解：圆的标准方程为x²+（y+1）²=4，圆心为（0，-1），半径R=2，
设直线和圆相交于AB，
若较短弧长与较长弧长之比为1：3，
则∠ACB=90°，
则圆心到直线x+y-k=0的距离d=

R

2

=

2

2

=

2

，
即d=

|-1-k|

2

=

|k+1|

2

=

2

，
即|k+1|=2，
解得k+1=2或k+1=-2，
解得k=1或k=-3，
故选：B

点评：本题主要考查直线和圆的位置关系的应用，根据条件得到圆心到直线的距离是

R

2

是解决本题的关键．