题目内容
20.设变量x,y满足约束条件$\left\{\begin{array}{l}{2x-y-2≤0}\\{x-2y+2≥0}\\{x+y-1≥0}\end{array}\right.$,则M=$\frac{y-x}{x+2}$的取值范围是( )| A. | [-$\frac{1}{3}$,$\frac{1}{2}$] | B. | [-$\frac{1}{2}$,1] | C. | [$\frac{1}{2}$,2] | D. | [$\frac{2}{3}$,$\frac{3}{2}$] |
分析 令y-x=n,x+2=m,则问题转化为在约束条件$\left\{\begin{array}{l}{m-n-4≤0}\\{m+2n-4≤0}\\{2m+n-5≥0}\end{array}\right.$之下,求M=$\frac{y-x}{x+2}$=$\frac{n}{m}$的取值范围,作出可行域由斜率公式数形结合可得.
解答 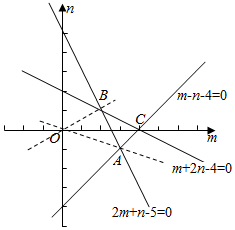 解:令y-x=n,x+2=m,则x=m-2,y=m+n-2,
解:令y-x=n,x+2=m,则x=m-2,y=m+n-2,
代入已知不等式组可得$\left\{\begin{array}{l}{m-n-4≤0}\\{m+2n-4≤0}\\{2m+n-5≥0}\end{array}\right.$,
作出可行域如图△ABC,M=$\frac{y-x}{x+2}$=$\frac{n}{m}$表示区域内的点与原点连线的斜率,
联方程组$\left\{\begin{array}{l}{m-n-4=0}\\{2m+n-5=0}\end{array}\right.$可解得A(3,-1),同理可得B(2,1),
当直线经过点A时,M取最小值-$\frac{1}{3}$,当直线经过点B时,M取最大值$\frac{1}{2}$.
故选:A.
点评 本题考查简单线性规划,换元法转化并利用数形结合的思想是解决问题的关键,属中档题.

练习册系列答案
相关题目
12.某学校有男学生400名,女学生600名.为了解男女学生在学习兴趣与业余爱好方面是否存在显著差异,拟从全体学生中抽取男学生40名,女学生60名进行调查,则这种抽样方法是( )
| A. | 抽签法 | B. | 随机数法 | C. | 系统抽样法 | D. | 分层抽样法 |
8.已知集合A={x|y=$\sqrt{2-x}}$},B={x|x2-2x<0},则( )
| A. | A∩B=∅ | B. | A∪B=R | C. | B⊆A | D. | A⊆B |
7.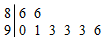 如图是某班8为学生诗词比赛得分的茎叶图,那么这8为学生得分的众数和中位数分别为( )
如图是某班8为学生诗词比赛得分的茎叶图,那么这8为学生得分的众数和中位数分别为( )
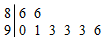 如图是某班8为学生诗词比赛得分的茎叶图,那么这8为学生得分的众数和中位数分别为( )
如图是某班8为学生诗词比赛得分的茎叶图,那么这8为学生得分的众数和中位数分别为( )| A. | 93,91 | B. | 86,93 | C. | 93,92 | D. | 86,91 |