题目内容
1.已知函数f0(x)=x(sinx+cosx),设fn(x)是fn-1(x)的导数,n∈N*.(1)求f1(x),f2(x)的表达式;
(2)写出fn(x)的表达式,并用数学归纳法证明.
分析 (1)根据导数的运算法则求导即可,
(2)先利用诱导公式,猜想猜想fn(x)=(x+n)sin(x+$\frac{nπ}{2}$)+(x-n)cos(x+$\frac{nπ}{2}$)(*),再根据数学归纳法证明即可.
解答 解:(1)f1(x)=f0′(x)=(sinx+cosx)+x(cosx-sinx)=(x-1)sin(-x)+(x+1)cosx,
f2(x)=f1′(x)=-sinx+(1-x)cosx+cosx-(1+x)sinx=-(2+x)sinx-(x-2)cosx,
(2)由(1)得f3(x)=f2′(x)=-(3+x)cosx+(x-3)sinx,
把f1(x),f2(x),f3(x),
f1(x)=(x+1)sin(x+$\frac{π}{2}$)+(x-1)cos(x+$\frac{π}{2}$),
f2(x)=(x+2)sin(x+$\frac{2π}{2}$)+(x-2)cos(x+$\frac{2π}{2}$),
f3(x)=(x+3)sin(x+$\frac{3π}{2}$)+(x-3)cos(x+$\frac{3π}{2}$),
猜想fn(x)=(x+n)sin(x+$\frac{nπ}{2}$)+(x-n)cos(x+$\frac{nπ}{2}$)(*),
下面用数学归纳法证明上述等式,
①当n=1时,由(1)可知,等式(*)成立,
②假设当n=k时,等式(*)成立,即fk(x)=(x+k)sin(x+$\frac{kπ}{2}$)+(x-k)cos(x+$\frac{kπ}{2}$),
则当n=k+1时,fk+1(x)=fk′(x)=sin(x+$\frac{kπ}{2}$)+(x+k)cosx+$\frac{kπ}{2}$)+cos(x+$\frac{kπ}{2}$)+(x-k)[-sin(x+$\frac{kπ}{2}$)],
=(x+k+1)cos(x+$\frac{kπ}{2}$)+[x-(k+1)][-sin(x+$\frac{kπ}{2}$)],
=(x+k+1)sin(x+$\frac{k+1}{2}$π)+[x-(k+1)]cos(x+$\frac{k+1}{2}$π),
即当n=k+1时,等式(*)成立
综上所述,当n∈N*,fn(x)=(x+n)sin(x+$\frac{nπ}{2}$)+(x-n)cos(x+$\frac{nπ}{2}$)成立.
点评 本题考查了导数的运算和诱导公式,以及数学归纳法,关键是利用诱导公式猜想出结论,属于难题.

| A. | 抽签法 | B. | 随机数法 | C. | 系统抽样法 | D. | 分层抽样法 |
| A. | 48 | B. | 24 | C. | 12 | D. | 6 |
| A. | A∩B=∅ | B. | A∪B=R | C. | B⊆A | D. | A⊆B |
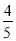 B.
B.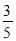 C.
C.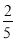 D.
D.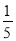

 为圆
为圆 的弦
的弦 的中点,则直线
的中点,则直线 的方程是( )
的方程是( ) B.
B.
 D.
D.