题目内容
下列各组集合中,满足P=Q的有 .(填序号)
①P={(1,2)},Q={(2,1)};
②P={1,2,3},Q={3,1,2};
③P={(x,y)|y=x-1,x∈R},Q={y|y=x-1,x∈R}.
①P={(1,2)},Q={(2,1)};
②P={1,2,3},Q={3,1,2};
③P={(x,y)|y=x-1,x∈R},Q={y|y=x-1,x∈R}.
考点:集合的相等
专题:集合
分析:根据集合元素的构成情况及集合相等的概念即可找出正确的序号.
解答:
解:①集合P含有一个元素(1,2),集合Q含有一个元素(2,1),(1,2),(2,1)表示不同的点,∴P≠Q;
②集合P,Q所含元素相同,只是顺序不同,∴P=Q;
③集合P的元素是点(x,y),Q的元素是实数y,∴P≠Q;
∴满足P=Q的有:②.
故答案为:②.
②集合P,Q所含元素相同,只是顺序不同,∴P=Q;
③集合P的元素是点(x,y),Q的元素是实数y,∴P≠Q;
∴满足P=Q的有:②.
故答案为:②.
点评:考查组成集合元素的情况,集合相等的概念.

练习册系列答案
相关题目
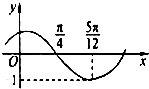 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<| π |
| 2 |
A、右平移
| ||
B、左平移
| ||
C、右平移
| ||
D、左平移
|