题目内容
2.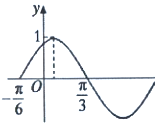 函数$f(x)=Asin({ωx+φ})({x∈R,A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,如果${x_1},{x_2}∈({-\frac{π}{6},\frac{π}{3}})$,且f(x1)=f(x2),则f(x1+x2)=( )
函数$f(x)=Asin({ωx+φ})({x∈R,A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,如果${x_1},{x_2}∈({-\frac{π}{6},\frac{π}{3}})$,且f(x1)=f(x2),则f(x1+x2)=( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
分析 由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.再由条件利用正弦函数的图象的对称性,求得f(x1+x2)的值.
解答 解:根据函数$f(x)=Asin({ωx+φ})({x∈R,A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象,可得A=1,$\frac{T}{2}$=$\frac{π}{ω}$=$\frac{π}{3}$+$\frac{π}{6}$,∴ω=2,
结合五点法作图可得2•(-$\frac{π}{6}$)+φ=0,∴φ=$\frac{π}{3}$,f(x)=sin(2x+$\frac{π}{3}$).
如果${x_1},{x_2}∈({-\frac{π}{6},\frac{π}{3}})$,且f(x1)=f(x2),结合2x+$\frac{π}{3}$∈(0,π),可得$\frac{{2x}_{1}+\frac{π}{3}+({2x}_{2}+\frac{π}{3})}{2}$=$\frac{π}{2}$,
∴x1+x2 =$\frac{π}{6}$,∴f(x1+x2)=f($\frac{π}{6}$)=sin($\frac{π}{3}$+$\frac{π}{3}$)=$\frac{\sqrt{3}}{2}$,
故选:C.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.还考查了正弦函数的图象的对称性,属于基础题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
12.${∫}_{-π}^{π}$sin2$\frac{x}{2}$dx=( )
| A. | 0 | B. | π-1 | C. | π | D. | π+1 |
10.已知$a=sin\frac{2π}{7}$,$b=cos\frac{12π}{7}$,$c=tan\frac{9π}{7}$,则( )
| A. | a>b>c | B. | c>b>a | C. | c>a>b | D. | a>c>b |
7.已知函数f(x)=f?($\frac{π}{4}$)cosx+sinx,则f($\frac{3π}{4}$)=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{2}$-1 | C. | 1 | D. | 0 |
14.将函数y=sin2x的图象向右平移$\frac{π}{6}$个单位,得到函数y=f(x)的图象,则f(x)=( )
| A. | $cos(2x-\frac{π}{6})$ | B. | $sin(2x-\frac{π}{6})$ | C. | $cos(2x-\frac{π}{3})$ | D. | $sin(2x-\frac{π}{3})$ |
11.集合A={x|x2-2x-3≤0},B={x|x>2},A∩B=( )
| A. | [-1,3] | B. | (2,3] | C. | [-1,+∞) | D. | (2,+∞) |
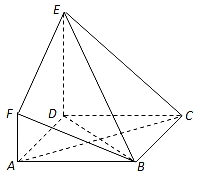 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.