题目内容
17．设函数f（x）=$\left\{\begin{array}{l}{{x}^{3}-3x，x≤a}\\{-2x，x＞a}\end{array}\right.$，若a=1，则f（x）的最大值为2．分析 利用导数判断f（x）的单调性，从而可求得f（x）的最大值．
解答 解：当a=1时，f′（x）=$\left\{\begin{array}{l}{3{x}^{2}-3，x≤1}\\{-2，x＞1}\end{array}\right.$，
令f′（x）=0得x=±1，
∴当x＜-1时，f′（x）＞0，当-x≥-1时，f′（x）≤0，
∴f（x）在（-∞，-1）上单调递增，在（-1，1）上单调递减，
∴当x=-1时，f（x）取得最大值f（-1）=（-1）3-3×（-1）=2．
故答案为：2．
点评 本题考查了函数单调性的判断与函数最值的计算，属于中档题．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
5．
某特色餐馆开通了美团外卖服务，在一周内的某特色外卖份数x（份）与收入y（元）之间有如下的对应数据：
（1）画出散点图；
（2）求回归直线方程；
（3）据此估计外卖份数为12份时，收入为多少元．
注：参考公式：$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{（\overline x）}^2}}}=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y}）}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}$，$\widehata$=$\overline y-\widehatb\overline x$；
参考数据：$\sum_{i=1}^5{x_1^2}=145，\sum_{i=1}^5{y_1^2}=13500，\sum_{i=1}^5{{x_i}{y_i}}=1380$．
某特色餐馆开通了美团外卖服务，在一周内的某特色外卖份数x（份）与收入y（元）之间有如下的对应数据：| 外卖份数x（份） | 2 | 4 | 5 | 6 | 8 |
| 收入y（元） | 30 | 40 | 60 | 50 | 70 |
（2）求回归直线方程；
（3）据此估计外卖份数为12份时，收入为多少元．
注：参考公式：$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{（\overline x）}^2}}}=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y}）}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}$，$\widehata$=$\overline y-\widehatb\overline x$；
参考数据：$\sum_{i=1}^5{x_1^2}=145，\sum_{i=1}^5{y_1^2}=13500，\sum_{i=1}^5{{x_i}{y_i}}=1380$．
2．
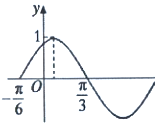函数$f（x）=Asin（{ωx+φ}）（{x∈R，A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的部分图象如图所示，如果${x_1}，{x_2}∈（{-\frac{π}{6}，\frac{π}{3}}）$，且f（x1）=f（x2），则f（x1+x2）=（ ）
函数$f（x）=Asin（{ωx+φ}）（{x∈R，A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的部分图象如图所示，如果${x_1}，{x_2}∈（{-\frac{π}{6}，\frac{π}{3}}）$，且f（x1）=f（x2），则f（x1+x2）=（ ）| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | 1 |