题目内容
已知△ABC的周长为36,B、C的坐标分别为(-8,0)和(8,0).
(1)求顶点A的轨迹方程;
(2)若∠BAC=90°,求△ABC的面积.
(1)求顶点A的轨迹方程;
(2)若∠BAC=90°,求△ABC的面积.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(1)由三角形的边角关系结合椭圆的定义求解;
(2)由椭圆定义结合三角形中的勾股定理求得|AB|•|AC|,则三角形的面积可求.
(2)由椭圆定义结合三角形中的勾股定理求得|AB|•|AC|,则三角形的面积可求.
解答:
解:(1)由题意知,|AB|+|AC|+|BC|=36,|BC|=16,
∴|AB|+|AC|=20>16,
则顶点A的轨迹是以B,C为焦点的椭圆,且2a=20,a=10,c=8.
∴b2=a2-c2=36.
∴顶点A的轨迹方程为:
+
=1(x≠±10);
(2)∵|AB|+|AC|=20,|BC|=16,
且∠BAC=90°,
∴|AB|2+|AC|2=(|AB|+|AC|)2-2|AB|•|AC|=|BC|2,
即202-162=2|AB|•|AC|,
∴|AB|•|AC|=72.
则△ABC的面积S=
×72=36.
∴|AB|+|AC|=20>16,
则顶点A的轨迹是以B,C为焦点的椭圆,且2a=20,a=10,c=8.
∴b2=a2-c2=36.
∴顶点A的轨迹方程为:
| x2 |
| 100 |
| y2 |
| 36 |
(2)∵|AB|+|AC|=20,|BC|=16,
且∠BAC=90°,
∴|AB|2+|AC|2=(|AB|+|AC|)2-2|AB|•|AC|=|BC|2,
即202-162=2|AB|•|AC|,
∴|AB|•|AC|=72.
则△ABC的面积S=
| 1 |
| 2 |
点评:本题考查了椭圆方程的求法,涉及椭圆上的点与焦点连线构成的三角形问题,常用椭圆定义、余弦定理结合求解,是压轴题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
下列结论错误的是( )
| A、命题p:“?x∈R,使得x2+x+1<0”,则¬P:?x∈R,x2+x+1≥0” | ||||
| B、“x=4”是“x2-3x-4=0”的充分非必要条件 | ||||
| C、数列2,5,11,20,x,47,…中的x=32 | ||||
D、已知a,b∈R+,2a+b=1,则
|
运行如图的程序框图相应的程序,输出的结果为( )


| A、-1 | |||||
B、
| |||||
C、
| |||||
D、
|
函数f(x)=
+
的零点个数为( )
| x2-2 |
| 3x |
| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
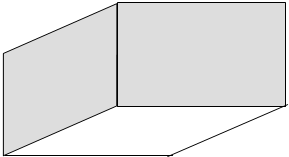 如图,用一块长为2米,宽为1米的矩形木板,在教室的墙角处围出一个直三棱柱的储物角(使木板垂直于地面的两边与墙面贴紧),试问应怎样围才能使储物角的容积最大?并求出这个最大值.
如图,用一块长为2米,宽为1米的矩形木板,在教室的墙角处围出一个直三棱柱的储物角(使木板垂直于地面的两边与墙面贴紧),试问应怎样围才能使储物角的容积最大?并求出这个最大值.