题目内容
函数f（x）=
+
的零点个数为（ ）
| x2-2 |
| 3x |
| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：把函数f（x）=
+
的零点个数，等价转化为函数y=2x2-4的图象和函数y=-3x的图象的交点个数，数形结合可得结论．
| x2-2 |
| 3x |
| 1 |
| 2 |
解答：
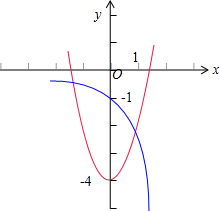解：函数f（x）=
+
的零点个数，
即方程函数
=-
的实数根的个数，
即方程2x2-4=-3x的实数根的个数，
即函数y=2x2-4的图象和函数y=-3x的图象的交点个数．
数形结合可得，函数y=2x2-4的图象（红色部分）
和函数y=-3x的图象（蓝色部分）的交点个数为2，
故答案为：2．
解：函数f（x）=| x2-2 |
| 3x |
| 1 |
| 2 |
即方程函数
| x2-2 |
| 3x |
| 1 |
| 2 |
即方程2x2-4=-3x的实数根的个数，
即函数y=2x2-4的图象和函数y=-3x的图象的交点个数．
数形结合可得，函数y=2x2-4的图象（红色部分）
和函数y=-3x的图象（蓝色部分）的交点个数为2，
故答案为：2．
点评：本题主要考查方程的根的存在性及个数判断，体现了化归与转化、数形结合的数学思想，属于基础
练习册系列答案
相关题目
对于方程[（
）|x|-
]2-|（
）|x|-
|-k=0的解，下列判断不正确的是（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
A、k＜-
| ||
| B、k=0时，2个解 | ||
C、-
| ||
| D、k＞0时，无解 |
下列对应能构成集合A到集合B的函数的是（ ）
A、A=Z，B=Q，对应法则f：x→y=
| ||||
| B、A={圆O上的点P}，B={圆O的切线}，对应法则：过P作圆O的切线 | ||||
| C、A=R，B=R，对应法则f：a→b=-2a2+4a-7，a∈A，b∈B | ||||
D、A={a|a为非零整数}，B={b|b=
|
已知集合M={x|x≥x2}，N={x|y=2x，x∈R}，则M∩N=（ ）
| A、（0，1） |
| B、[0，1] |
| C、[0，1） |
| D、（0，1] |
已知数列{an}的前n项和为Sn，若an=
，则S10=（ ）
| 2 |
| n(n+2) |
A、
| ||
B、
| ||
C、
| ||
D、
|