题目内容
不等式x2-3x＜0的解集是（ ）
| A、（-∞，0） |
| B、（0，3） |
| C、（-∞，0）∪（3，+∞） |
| D、（3，+∞） |
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：原不等式可化为：x（x-3）＜0，可得其对应方程的根，进而可得解集．
解答：
解：不等式x2-3x＜0可化为：
x（x-3）＜0，
故解集为{x|0＜x＜3}
故选：B．
x（x-3）＜0，
故解集为{x|0＜x＜3}
故选：B．
点评：本题考查一元二次不等式的解集，因式分解是解决问题的关键，属基础题．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
以圆x2-2x+y2=0的圆心为圆心，半径为2的圆的方程（ ）
| A、（x+1）2+y2=2 |
| B、（x-1）2+y2=2 |
| C、（x+1）2+y2=4 |
| D、（x-1）2+y2=4 |
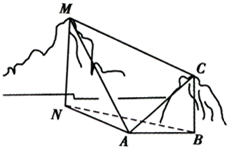如图，为测量山高MN，选择A和另一座山的山顶C为测量观测点．从A点测得M点的仰角∠MAN=60°，C点的仰角∠CAB=45°以及∠MAC=75°；从C点测得∠MCA=60°．已知山高BC=100m，求山高MN．在△ABC中，角A、B、C所对的边分别为a、b、c，若a=8，b=10，A=45°，满足条件的三角形有（ ）
| A、0个 | B、1个 | C、2个 | D、无数个 |