题目内容
设p:实数x满足x2-5ax+4a2<0(其中a>0),q:实数x满足2<x≤5
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若?q是?p的必要不充分条件,求实数a的取值范围.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若?q是?p的必要不充分条件,求实数a的取值范围.
考点:复合命题的真假,必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:(1)将a=1代入,求出关于p的范围,从而求出p且q的范围;(2)由题意得不等式组,解出即可.
解答:
解:(1)当a=1时,解得1<x<4,
即p为真时实数x的范围是:1<x<4,
若p∧q为真,则P真且q真,
∴实数x的范围是(2,4);
(2)若?q是?p的必要不充分条件,
即p是q的必要不充分条件,
设A={x|p(x)},B={x|q(x)},则B?A,
由x2-5ax+4a2<0得(x-4a)(x-a)<0,
∵a>0,∴A=(a,4a),
又B=(2,5],则a≤2且4a>5,
解得:
<a≤2.
即p为真时实数x的范围是:1<x<4,
若p∧q为真,则P真且q真,
∴实数x的范围是(2,4);
(2)若?q是?p的必要不充分条件,
即p是q的必要不充分条件,
设A={x|p(x)},B={x|q(x)},则B?A,
由x2-5ax+4a2<0得(x-4a)(x-a)<0,
∵a>0,∴A=(a,4a),
又B=(2,5],则a≤2且4a>5,
解得:
| 5 |
| 4 |
点评:本题考查了复合命题的真假,考查了充分必要条件,是一道中档题.

练习册系列答案
相关题目
计算:(log213)3+(log217)3+3log213log217=( )
| A、0 | B、1 | C、-1 | D、2 |
在△ABC中,角A、B、C所对的边分别为a、b、c,若a=8,b=10,A=45°,满足条件的三角形有( )
| A、0个 | B、1个 | C、2个 | D、无数个 |
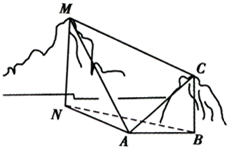 如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,求山高MN.
如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,求山高MN.