题目内容
在△ABC中，A=60°，b=8，S△ABC=6
，则
= ．
| 3 |
| a+b |
| sinA+sinB |
考点：正弦定理
专题：解三角形
分析：首先利用三角形的面积公式求出c的值，进一步利用余弦定理求出a的值，最后利用正弦定理和等比性质求出结果．
解答：
解：已知：S△ABC=6
所以：
bcsinA=6
解得：c=3
进一步利用余弦定理：a2=b2+c2-2bccosA
解得：a=7
所以：
=
=
=
故答案为：
| 3 |
所以：
| 1 |
| 2 |
| 3 |
解得：c=3
进一步利用余弦定理：a2=b2+c2-2bccosA
解得：a=7
所以：
| a |
| sinA |
| b |
| sinB |
| a+b |
| sinA+sinB |
14
| ||
| 3 |
故答案为：
14
| ||
| 3 |
点评：本题考查的知识要点：三角形的面积公式，正弦和余弦定理得应用．
练习册系列答案
相关题目
计算：（log213）3+（log217）3+3log213log217=（ ）
| A、0 | B、1 | C、-1 | D、2 |
某几何体的三视图如图所示，则该几何体的体积为（ ）
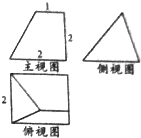
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
以圆x2-2x+y2=0的圆心为圆心，半径为2的圆的方程（ ）
| A、（x+1）2+y2=2 |
| B、（x-1）2+y2=2 |
| C、（x+1）2+y2=4 |
| D、（x-1）2+y2=4 |
下列命题是真命题的是（ ）
A、?x∈R使得sinxcosx=
| ||
| B、?x∈（-∞，0）使得2x＞1 | ||
| C、?x∈R恒有sinx＞cosx | ||
| D、?x∈（0，π）恒有x2＞x-1 |
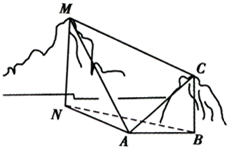如图，为测量山高MN，选择A和另一座山的山顶C为测量观测点．从A点测得M点的仰角∠MAN=60°，C点的仰角∠CAB=45°以及∠MAC=75°；从C点测得∠MCA=60°．已知山高BC=100m，求山高MN．