题目内容
已知f(x)=x|x-a|+b,x∈R.
(1)当a=1,b=1时.f(2x)=
,求x的值;
(2)若b<0,b为常数,任意x∈[0,1],不等式f(x)<0恒成立,求实数a的取值范围.
(1)当a=1,b=1时.f(2x)=
| 5 |
| 4 |
(2)若b<0,b为常数,任意x∈[0,1],不等式f(x)<0恒成立,求实数a的取值范围.
考点:函数恒成立问题
专题:函数的性质及应用
分析:利用换元法将函数转化为关于t的一元二次函数,利用指数函数的图象和性质即可求出方程的解.将不等式恒成立转化为求函数的最值即可得到结论.
解答:
解:(1)当a=1,b=1时,f(x)=x|x-a|+b=x|x-1|+1,
若x≥1时,则f(x)=x2-x+1,
当x<1时,f(x)=-x2+x+1,
设t=2x,
若x≥0,则t≥1,
此时由f(2x)=
,得t2-t+1=
,
即(t-
)2=
,
∴t=
+
=
,
∴x=log2
.
当x<0时,t<1,
此时由f(2x)=
,得-t2+t+1=
,
即-(t-
)2+
=
,
∴t=
,∴x=log2
=-1.
(2)∵b<0
∴当x=0时,f(x)=b<0恒成立,∴a∈R
当0<x≤1时,f(x)<0,即|x2-ax|<b,
∴b<x2-ax<-b,
∴(x+
)max<x<(x-
)min恒成立
令g(x)=x+
,则当b<0时,g(x)在[0,1]上是增函数,
∴a>gmax=g(1)=1+b,
令h(x)=x-
,当-1≤b<0时,在(0,1]上x-
=x+
≥2
,
当x=
时,取得最小值2
,此时要使a存在,则满足
,即-1≤b<-3+2
,
当b<-1时,在(0,1]上h(x)=x-
,为减函数,当x=1时,函数取得最小值,∴(x-
)min=1-b,
综上所述,当-1≤b<-3+2
时,a的取值范围是(1+b,2
),
当b<-1时,a的取值范围是(1+b,1-b).
若x≥1时,则f(x)=x2-x+1,
当x<1时,f(x)=-x2+x+1,
设t=2x,
若x≥0,则t≥1,
此时由f(2x)=
| 5 |
| 4 |
| 5 |
| 4 |
即(t-
| 1 |
| 2 |
| 1 |
| 2 |
∴t=
| 1 |
| 2 |
| ||
| 2 |
1+
| ||
| 2 |
∴x=log2
1+
| ||
| 2 |
当x<0时,t<1,
此时由f(2x)=
| 5 |
| 4 |
| 5 |
| 4 |
即-(t-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴t=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵b<0
∴当x=0时,f(x)=b<0恒成立,∴a∈R
当0<x≤1时,f(x)<0,即|x2-ax|<b,
∴b<x2-ax<-b,
∴(x+
| b |
| x |
| b |
| x |
令g(x)=x+
| b |
| x |
∴a>gmax=g(1)=1+b,
令h(x)=x-
| b |
| x |
| b |
| x |
| -b |
| x |
| -b |
当x=
| -b |
| -b |
|
| 2 |
当b<-1时,在(0,1]上h(x)=x-
| b |
| x |
| b |
| x |
综上所述,当-1≤b<-3+2
| 2 |
| -b |
当b<-1时,a的取值范围是(1+b,1-b).
点评:本题主要考查与指数函数有关的指数方程的求解,利用换元法是解决指数型方程的基本方法,将不等式恒成立转化为求函数的最值是解决不等式恒成立的常用方法.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
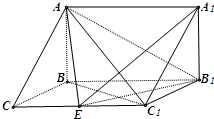 如图,在三棱柱ABC-A1B1C1中,已知BC=1,BB1=2,∠BCC1=90°,AB⊥侧面BB1C1C.
如图,在三棱柱ABC-A1B1C1中,已知BC=1,BB1=2,∠BCC1=90°,AB⊥侧面BB1C1C.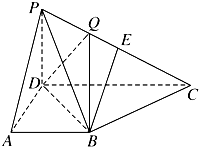 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,若 E为PC的中点,且BE与平面PDC所成的角的正弦值为
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,若 E为PC的中点,且BE与平面PDC所成的角的正弦值为