题目内容
已知p:?x∈R,x2+mx-m+3>0;q:?x0∈R,x02+2x0-m-1=0,若p∧q为真命题,求实数m的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:利用一元二次不等式、一元二次方程的解集与判别式的关系化简命题p,q,由p∧q为真命题,则p与q都为真命题,即可得出.
解答:
解:p:?x∈R,x2+mx-m+3>0,则△=m2-4(3-m)<0,解得-6<m<2;
q:?x0∈R,x02+2x0-m-1=0,则△1=4-4(-m-1)≥0,解得m≥-2.
若p∧q为真命题,则p与q都为真命题,
∴
,
解得-2≤m<2.
∴实数m的取值范围是-2≤m<2.
q:?x0∈R,x02+2x0-m-1=0,则△1=4-4(-m-1)≥0,解得m≥-2.
若p∧q为真命题,则p与q都为真命题,
∴
|
解得-2≤m<2.
∴实数m的取值范围是-2≤m<2.
点评:本题考查了一元二次不等式、一元二次方程的解集与判别式的关系、复合命题的判定,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
如果二次函数f(x)=3x2+bx+1的图象关于直线x=
对称,则b的值为( )
| 1 |
| 2 |
| A、-1 | B、1 | C、-3 | D、3 |
执行如图的程序框图,算法执行完毕后,输出的S为( )


| A、8 | B、63 | C、92 | D、129 |
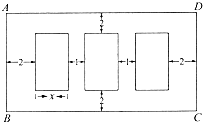 某公司因业务发展需要,准备印制如图所示的宣传彩页,宣传彩页有三幅大小相同的三个画面组成,每个画面的面积都是200cm2,这三个画面中都要绘制半径为5cm的圆形图案,为美观起见,每两个画面之间要留1cm的空白,三幅画周围要留2cm页边距,如图,设一边长x,所选用的彩页纸张面积为S
某公司因业务发展需要,准备印制如图所示的宣传彩页,宣传彩页有三幅大小相同的三个画面组成,每个画面的面积都是200cm2,这三个画面中都要绘制半径为5cm的圆形图案,为美观起见,每两个画面之间要留1cm的空白,三幅画周围要留2cm页边距,如图,设一边长x,所选用的彩页纸张面积为S