题目内容
19.已知数列{an}满足a1=2,an+1=an2-nan+1,则an=n+1.分析 a1=2,an+1=an2-nan+1,可得a2=3,a3=4,a4=5,…,猜想an=n+1.再利用数学归纳法证明即可.
解答 解:∵a1=2,an+1=an2-nan+1,
∴a2=22-2+1=3,a3=4,a4=5,…,
猜想an=n+1.
下面利用数学归纳法证明:
(1)当n=1时,a1=2;
(2)假设n=k(k∈N*)时,ak=k+1成立,
则n=k+1,ak+1=${a}_{k}^{2}-k{a}_{k}$+1=(k+1)2-k(k+1)+1=k+1+1.
∴当n=k+1时猜想成立.
综上可得:?n∈N*,都有an=n+1.
故答案为:n+1.
点评 本题考查了数学归纳法、递推关系,考查了猜想推理能力与计算能力,属于中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
9.已知公比为q的等比数列{an},且满足条件|q|>1,a2+a7=2,a4a5=-15,则a12=( )
| A. | -$\frac{27}{25}$ | B. | -$\frac{25}{3}$ | C. | -$\frac{27}{25}$或-$\frac{25}{3}$ | D. | $\frac{25}{3}$ |
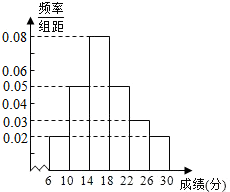 某省去年高三200000考生英语听力考试成绩服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如下方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30],如图是按上述分组方法得到的频率分布直方图.
某省去年高三200000考生英语听力考试成绩服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如下方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30],如图是按上述分组方法得到的频率分布直方图.