题目内容
7.已知圆锥的侧面积为2π,底面积为π,则该圆锥的内接圆柱体积的最大值为$\frac{8π}{27}$.分析 设内接圆柱的底面半径为r,高为h,根据三角形相似找出h与r的关系,然后表示出内接圆柱的体积,最后利用基本不等式求出最值即可,注意等号成立的条件.
解答 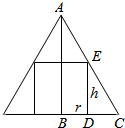 解:圆锥的侧面积为2π,底面积为π,
解:圆锥的侧面积为2π,底面积为π,
设内接圆柱的底面半径为r,高为h,则圆锥的底面半径1,圆锥的母线长为:l=2,圆锥的高为:$\sqrt{3}$,如右图,
∵△CAB∽△CED,
∴$\frac{ED}{AB}$=$\frac{CD}{CB}$,即$\frac{h}{2}$=$\frac{1-r}{1}$,则h=2-2r,
∴内接圆柱的体积为:
V=πr2h=πr2×(2-2r)=πr•r•(2-2r)≤π($\frac{r+r+2-2r}{3}$)3=$\frac{8π}{27}$,
当且仅当r=2-2r,即r=$\frac{2}{3}$时取等号,
∴内接圆柱体积的最大值是$\frac{8π}{27}$.
故答案为:$\frac{8π}{27}$.
点评 本题主要考查了圆锥的内接圆柱的体积,以及基本不等式在最值中的应用,同时考查了分析问题的能力,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
17.化简log2$\sqrt{2\sqrt{2\sqrt{2\sqrt{2}…\sqrt{2}}}}$(总共有2015个2)的结果为( )
| A. | $\frac{2014}{2015}$ | B. | $\frac{{2}^{2015}-1}{{2}^{2015}}$ | C. | $\frac{{2}^{2014}-1}{{2}^{2014}}$ | D. | $\frac{{2}^{2016}-1}{{2}^{2016}}$ |
15.已知奇函数f(x)对任意正实数x1,x2(x1≠x2),恒有$\frac{{f(x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0,则一定正确的是( )
| A. | f(4)>f(-6) | B. | f(-4)<f(-6) | C. | f(-4)>f(-6) | D. | f(4)<f(-6) |
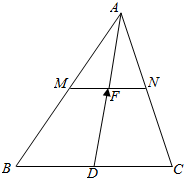 在△ABC中,已知A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于点F,求$\overrightarrow{DF}$的坐标.
在△ABC中,已知A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于点F,求$\overrightarrow{DF}$的坐标.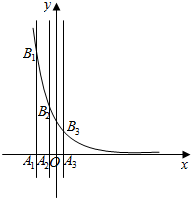 (理)已知等差数列{an}的首项为p,公差为d(d>0),对于不同的自然数n(n∈N*),直线x=an与x轴和指数函数f(x)=($\frac{1}{2}$)x的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.
(理)已知等差数列{an}的首项为p,公差为d(d>0),对于不同的自然数n(n∈N*),直线x=an与x轴和指数函数f(x)=($\frac{1}{2}$)x的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.