题目内容
已知cos（30°-α）=
且30°＜α＜120°，那么cos（α+240°）= ．
| 5 |
| 13 |
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：直接利用诱导公式化简求解即可．
解答：
解：cos（α+240°）=cos（α+270°-30°）=-sin（30°-α）．
∵cos（30°-α）=
，30°＜α＜120°，
∴30°-α∈（-90°，0°）
∴sin（30°-α）=-
=-
．
∴cos（α+240°）=-sin（30°-α）=
．
故答案为：
．
∵cos（30°-α）=
| 5 |
| 13 |
∴30°-α∈（-90°，0°）
∴sin（30°-α）=-
| 1-cos2(30°-α) |
| 12 |
| 13 |
∴cos（α+240°）=-sin（30°-α）=
| 12 |
| 13 |
故答案为：
| 12 |
| 13 |
点评：本题考查诱导公式的应用三角函数的化简求值，基本知识的考查．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
命题“对任意实数x∈[1，2]，关于x的不等式x2-a≤0恒成立”为真命题的一个必要不充分条件是（ ）
| A、a≥4 | B、a≤4 |
| C、a≥3 | D、a≤3 |
已知集合A={y|y=sinx}，B={x|（x+3）（2x-1）≤0}，则A∩B=（ ）
A、[-3，
| ||
B、[-1，
| ||
C、[-1，
| ||
D、（-3，
|
已知集合A=[-1，1]，B={x|（x+3）（2x-1）≤0}，则A∩B=（ ）
A、[-3，
| ||
B、[-1，
| ||
C、[-1，
| ||
D、（-3，
|
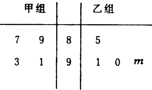如图所示茎叶图记录了甲、乙两学习小组各4名同学在某次考试中的数学成绩，乙组记录中有一个数字模糊，无法确认，假设这个数字具有随机性，并在图中用m（m∈N）表示．