若x＞1.那么1og2x+31ogx4的最小值是2$\sqrt{6}$．题目和参考答案——青夏教育精英家教网—

题目内容

6．若x＞1，那么1og₂x+31og_x4的最小值是2$\sqrt{6}$．

分析利用对数换底公式、基本不等式的性质即可得出．

解答解：x＞1，∴lgx＞0．
1og₂x+31og_x4=$\frac{lgx}{lg2}$+$\frac{6lg2}{lgx}$≥2$\sqrt{6}$，当且仅当x=${2}^{\sqrt{6}}$时取等号．
故答案为：2$\sqrt{6}$．

点评本题考查了对数换底公式、基本不等式的性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案

相关题目

6．执行如图所示程序框图，若输出的S=-46，则①处填入的条件可以是（　　）

7．

为研究男女同学空间想象能力的差异，孙老师从高一年级随机选取了20名男生、20名女生，进行空间图形识别测试，得到成绩茎叶图如下，假定成绩大于等于80分的同学为“空间想象能力突出”，低于80分的同学为“空间想象能力正常”．
（1）完成下面2×2列联表，并判断是否有90%的把握认为“空间想象能力突出”与性别有关；

	空间想象能力突出	空间想象能力正常	合计
男生
女生
合计

（2）从“空间想象能力突出”的同学中随机选取男生2名、女生2名，记其中成绩超过90分的人数为ξ，求随机变量ξ的分布列和数学期望．
下面公式及临界值表仅供参考：${X^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$

P（X²≥k）	0.100	0.050	0.010
k	2.706	3.841	6.635

4．

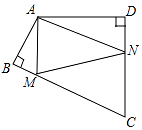如图，四边形ABCD中，∠BAD=120°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN周长最小时，则∠AMN+∠ANM的度数为（　　）

1．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦距为2$\sqrt{3}$，点（$\sqrt{2}$，-$\frac{\sqrt{2}}{2}$）在C 上．
（Ⅰ）求椭圆C的方程
（Ⅱ）设点（2x，y）在C上，点（x，y）的轨迹为曲线E，过原点作直线l与曲线E交于A，B两点，点D （-2，0），证明：$\overrightarrow{DA}$•$\overrightarrow{DB}$为定值，并求出定值．

11．下列各式中正确的个数是（　　）
①（x⁷）′=7x⁶； ②（x^-1）′=x^-2； ③（$\frac{1}{\sqrt{x}}$）′=-$\frac{1}{2}$x${\;}^{-\frac{3}{2}}$； ④（$\root{5}{{x}^{2}}$）′=$\frac{2}{5}$x${\;}^{-\frac{3}{5}}$； ⑤（cosx）′=-sinx；
⑥（cos2）′=-sin2．

18．已知函数f（x）=（2-a）lnx+$\frac{1}{x}$+2ax（a≤0）．
（1）当a=0时，求f（x）在x=1处的切线方程；
（2）当a＜0时，讨论f（x）的单调性；
（3）若?a∈（-3，-2），x₁，x₂∈[1，3]，有（m+ln3）a-2ln3＞|f（x₁）-f（x₂）|，求实数m的取值范围．

15．

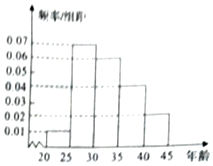某地为增强居民的传统文化意识，活跃节日氛围，在元宵节举办了猜灯谜比赛，现从参加比赛的选手中随机抽取200名后按年龄分组：第1组[20，25），第2组[25，30），第3组[30，35），第4组[35，40），第5组[40，45），得到的频率分布直方图如图所示．
（1）若从第3，4，5组中用分层抽样的方法抽取12名选手参加传统知识问答比赛，则应从第3，4，5组各抽取多少名选手？
（2）在（1）的条件下，该地决定在第4，5组的选手中随机抽取2名选手介绍比赛感想，求第5组至少有一名选手被抽中的概率．

16．下列命题中正确的有（　　）
①设有一个回归方程$\stackrel{∧}{y}$=2-3x，变量x增加一个单位时，y平均增加3个单位；
②命题p：“?x₀∈R，x₀²-x₀-1＞0”的否定￢p“?x∈R，x²-x-1≤0”；
③残差平方和越小的模型，拟合的效果越好；
④用相关指数R²=1-$\frac{\sum_{i=1}^{n}（{y}_{i}-\stackrel{∧}{{y}_{i}}）^{2}}{\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^{2}}$来刻画回归效果，R²的值越小，说明模型的拟合效果越好．

试题分类