题目内容
12．已知条件p：（1-x）（x+1）＞0，条件q：-1＜x≤1，则￢p是￢q的必要不充分条件．分析 条件p：（1-x）（x+1）＞0，解得-1＜x＜1，可得q是p的必要不充分条件，即可得出结论．
解答 解：条件p：（1-x）（x+1）＞0，解得-1＜x＜1，条件q：-1＜x≤1，
∴q是p的必要不充分条件，
则￢p是￢q的必要不充分条件．
故答案为：必要不充分条件．
点评 本题考查了不等式的解法、充要条件的判定方法，考查了推理能力与计算能力，属于基础题．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
2．图（1）、图（2）、图（3）、图（4）分别包含1、5、13和25个互不重叠的单位正方形，按同样的方式构造图形，则第n个图包含（ ）个互不重叠的单位正方形．
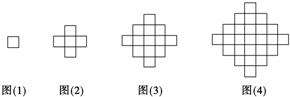
| A． | n2-2n+1 | B． | 2n2-2n+1 | C． | 2n2+2 | D． | 2n2-n+1 |
4．若函数y=f（x）的图象与函数y=sin（x+$\frac{π}{4}$）的图象关于P（$\frac{π}{2}$，0）对称，则f（x）解析式为（ ）
| A． | f（x）=sin（x-$\frac{π}{4}$） | B． | f（x）=-sin（x-$\frac{π}{4}$） | C． | f（x）=-cos（x+$\frac{π}{4}$） | D． | f（x）=cos（x-$\frac{π}{4}$） |