题目内容
4.若函数y=f(x)的图象与函数y=sin(x+$\frac{π}{4}$)的图象关于P($\frac{π}{2}$,0)对称,则f(x)解析式为( )| A. | f(x)=sin(x-$\frac{π}{4}$) | B. | f(x)=-sin(x-$\frac{π}{4}$) | C. | f(x)=-cos(x+$\frac{π}{4}$) | D. | f(x)=cos(x-$\frac{π}{4}$) |
分析 根据y=f(x)图象关于点($\frac{π}{2}$,0)的对称图象对应的函数解析式为y=-f(π-x),得出结论.
解答 解:由于点(x,y)关于点($\frac{π}{2}$,0)的对称点为(π-x,-y),
故有y=f(x)图象关于点($\frac{π}{2}$,0)的对称图象对应的函数解析式为y=-f(π-x),
故把函数y=sin(x+$\frac{π}{4}$)的图象关于P($\frac{π}{2}$,0)对称,可得y=-sin[(π-x)+$\frac{π}{4}$],
故f(x)=-sin[(π-x)+$\frac{π}{4}$]=sin($\frac{π}{4}$-x)=-sin(x-$\frac{π}{4}$),
故选:B.
点评 本题主要考查两个函数关于($\frac{π}{2}$,0)的对称的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.用分析法证明问题时是从要证明的结论出发,逐步寻求使它成立的( )
| A. | 充要条件 | B. | 充分条件 | ||
| C. | 必要条件 | D. | 既不充分也不必要条件 |
14.函数y=sin(x+$\frac{π}{6}$)的一个递减区间是( )
| A. | [-$\frac{π}{2}$,$\frac{π}{2}$] | B. | [-π,0] | C. | [-$\frac{2π}{3}$,$\frac{2π}{3}$] | D. | [$\frac{π}{3}$,$\frac{4π}{3}$] |
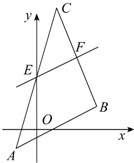 已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,且E、F分别是AC、BC的中点.求:
已知△ABC的三顶点是A(-1,-1),B(3,1),C(1,6).直线l平行于AB,交AC,BC分别于E,F,且E、F分别是AC、BC的中点.求: