题目内容
已知函数y=f（x）是R上的奇函数，其零点为x1，x2，…x2015，则x1+x2+…+x2015= ．
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：先由函数f（x）是定义在R上的奇函数确定0是一个零点，根据奇函数的对称性，得出其他非0的零点关于原点对称，从而得出所有零点的和．
解答：
解：∵f（x）是R上的奇函数，
∴0是函数y=f（x）的零点．
其他非0的2014个零点关于原点对称．
∴x1+x2+…+x2015=0．
故答案为：0．
∴0是函数y=f（x）的零点．
其他非0的2014个零点关于原点对称．
∴x1+x2+…+x2015=0．
故答案为：0．
点评：函数的奇偶性是函数最重要的性质之一，奇函数的图象关于原点对称，利用对称性解题是往往是解题的突破口．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
三个数a=0.22，b=log
2，c=20.2之间的大小关系是（ ）
| 1 |
| 3 |
| A、a＜c＜b |
| B、b＜a＜c |
| C、a＜b＜c |
| D、b＜c＜a |
已知集合A={y|y=2sin（2x-
）+1，x∈（-
，
）}，集合B={x|y=lg（x2+x）}，设全集U=R，则A∩（∁UB）等于（ ）
| π |
| 3 |
| π |
| 12 |
| π |
| 2 |
| A、[3，+∞） |
| B、（-1，0] |
| C、（3，+∞） |
| D、[-1，0] |
函数f（x）（x∈R）的图象如图所示，则函数g（x）=f（log
x）的单调减区间是（ ）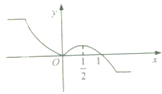
| 1 |
| 4 |
A、[0，
| ||||||
B、（-∞，0）∪[
| ||||||
C、[
| ||||||
D、[
|
数列{an}的各项为正数，其前n项和Sn=4-(
)n-2（n∈N*）．若Tn=a1a2+a2a3+…+anan+1（n∈N*），则Tn的取值所在的区间最恰当的是（ ）
| 1 |
| 2 |
A、(0，
| ||
| B、[2，4） | ||
C、[2，
| ||
| D、（0，4） |
在下列各数中，最大的数是（ ）
| A、11111（2） |
| B、1000（4） |
| C、210（6） |
| D、85（9） |