题目内容
全称命题“所有被7整除的整数都是奇数”的否定（ ）
| A、存在一个被7整除的整数不是奇数 |
| B、存在一个奇数，不能被7整除 |
| C、所有被7整除的整数都不是奇数 |
| D、所有奇数都不能被7整除 |
考点：命题的否定
专题：简易逻辑
分析：直接利用全称命题的否定是特称命题写出结果即可．
解答：
解：全称命题的否定是特称命题，
所以全称命题“所有被7整除的整数都是奇数”的否定：存在一个被7整除的整数不是奇数．
故选：A．
所以全称命题“所有被7整除的整数都是奇数”的否定：存在一个被7整除的整数不是奇数．
故选：A．
点评：本题考查命题的否定全称命题与特称命题的否定关系，基本知识的考查．
练习册系列答案
相关题目
函数f（x）=log2（-x2+ax+3）在（2，4）是单调递减的，则a的范围是（ ）
A、（
| ||
B、[
| ||
| C、[8，+∞） | ||
| D、（-∞，4] |
三个数a=0.22，b=log
2，c=20.2之间的大小关系是（ ）
| 1 |
| 3 |
| A、a＜c＜b |
| B、b＜a＜c |
| C、a＜b＜c |
| D、b＜c＜a |
函数f（x）（x∈R）的图象如图所示，则函数g（x）=f（log
x）的单调减区间是（ ）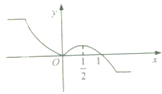
| 1 |
| 4 |
A、[0，
| ||||||
B、（-∞，0）∪[
| ||||||
C、[
| ||||||
D、[
|
数列{an}的各项为正数，其前n项和Sn=4-(
)n-2（n∈N*）．若Tn=a1a2+a2a3+…+anan+1（n∈N*），则Tn的取值所在的区间最恰当的是（ ）
| 1 |
| 2 |
A、(0，
| ||
| B、[2，4） | ||
C、[2，
| ||
| D、（0，4） |
不等式x（2-x）＞0的解集是（ ）
| A、{x|0＜x＜2} |
| B、{x|-2＜x＜0} |
| C、{x|x＜-2或x＞0} |
| D、∅ |