题目内容
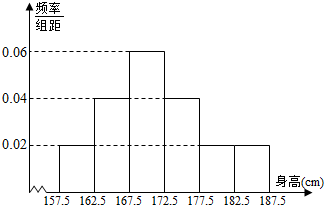
8.生产一批零件,其质量按测试指标划分为:指标大于或等于8为优质品,小于8大于等于4为正品,小于4为次品,现随机抽取这种零件100件进行检测,检测结果统计如下:据以上述测试中各组的频率作为相应的概率.| 测试指标 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10) |
| 零件数 | 2 | 8 | 32 | 38 | 20 |
(2)生产一件零件,若是优质品可盈利40元,若是正品盈利20元,若是次品则亏损20元,若从大量的零件中随机抽取2件,其利润之和记为x(单位:元),求x的分布列及数学期望.
分析 (1)利用组中值,估计这种零件的平均质量指标;
(2)由题意知x的可能取值为80,60,40,20,-40,0,分别求出相应的概率,由此能求出x的分布列及数学期望.
解答 解:(1)这种零件的平均质量指标$\frac{1}{100}$[1×2+3×8+5×32+7×38+9×20]=6.32;
(2)优质品的概率为0.2,正品的概率为0.7,次品的概率为0.1,
x的取值为80,60,40,20,-40,0.
P(x=80)=0.2×0.2=0.04,P(x=60)=0.7×0.2×2=0.28,
P(x=40)=0.7×0.7=0.49.P(x=20)=0.2×0.1×2=0.04,
P(x=-40)=0.1×0.1=0.01,P(x=0)=0.7×0.1×2=0.14,
所以x的分布列为:
| x | 80 | 60 | 40 | 20 | -40 | 0 |
| P | 0.04 | 0.28 | 0.49 | 0.04 | 0.01 | 0.14 |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是历年高考的必考题型,是中档题.

练习册系列答案
相关题目
16.在平面直角坐标系xOy中,若曲线y=2x2+$\frac{a}{x}$(a是常数)过点P(-1,-30),则函数y=2x2+$\frac{a}{x}$在区间[1,4]的最大值与最小值的和为64.
17.已知菱形ABCD的边长为为4,∠ABC=$\frac{π}{3}$,向其内部随机投放一点P,则点P与菱形各顶点距离均大于1的概率为( )
| A. | 1-$\frac{\sqrt{3}π}{24}$ | B. | 1-$\frac{\sqrt{3}π}{12}$ | C. | $\frac{\sqrt{3}π}{24}$ | D. | $\frac{\sqrt{3}π}{12}$ |
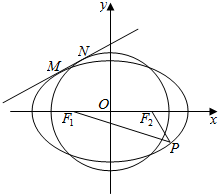 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,P为椭圆C上任意一点,当|PF1|-|PF2|取最大值时,|PF1|=3,|PF2|=1.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,P为椭圆C上任意一点,当|PF1|-|PF2|取最大值时,|PF1|=3,|PF2|=1.