题目内容
3.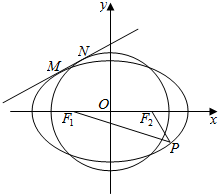 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,P为椭圆C上任意一点,当|PF1|-|PF2|取最大值时,|PF1|=3,|PF2|=1.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,P为椭圆C上任意一点,当|PF1|-|PF2|取最大值时,|PF1|=3,|PF2|=1.(1)求椭圆C的方程;
(2)设直线l与椭圆C、圆x2+y2=r2均相切,切点分别为M、N,当r在区间(b,a)内变化时,求|MN|的最大值.
分析 (1)运用椭圆的焦半径公式和椭圆的范围,可得2c=2,再由椭圆的定义可得2a=4,求得b,进而得到椭圆的方程;
(2)设直线l的方程为y=kx+m,联立椭圆方程,得(3+4k2)x2+8kmx+4m2-12=0,由此利用根的判别式为0,再由直线和圆相切的条件:d=r,结合勾股定理,以及基本不等式即可得到所求最大值.
解答 解:(1)|PF1|-|PF2|=a+exP-(a+exP)=2exP,
当xP取得最大值a时,|PF1|-|PF2|取最大值.
且有2ea=2,即$\frac{c}{a}$•a=1,即c=1,
又|PF1|+|PF2|=4,即2a=4,即a=2,
b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{3}$,
则椭圆C的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)由题意得直线l的斜率存在,设直线l的方程为y=kx+m,
即kx-y+m=0,设M(x1,y1),N(x2,y2),
∵直线l与圆x2+y2=r2相切,
∴$\frac{|m|}{\sqrt{1+{k}^{2}}}$=r,即m2=r2(k2+1),①
联立$\left\{\begin{array}{l}{y=kx+m}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$,得(3+4k2)x2+8kmx+4m2-12=0,
由直线l与椭圆相切,得△=64k2m2-4(3+4k2)(4m2-12)=0,
即m2=4k2+3,②
由①②得k2=$\frac{{r}^{2}-3}{4-{r}^{2}}$,m2=$\frac{{r}^{2}}{4-{r}^{2}}$,
设点M(x0,y0),则x02=($\frac{4km}{3+4{k}^{2}}$)2=$\frac{16{k}^{2}}{3+4{k}^{2}}$=$\frac{16({r}^{2}-3)}{{r}^{2}}$,
y02=$\frac{1}{4}$(12-3x02)=$\frac{9(4-{r}^{2})}{{r}^{2}}$,
∴|OM|2=$\frac{7{r}^{2}-12}{{r}^{2}}$,
∴|MN|2=|OM|2-|ON|2=$\frac{7{r}^{2}-12}{{r}^{2}}$-r2
=7-(r2+$\frac{12}{{r}^{2}}$),
∵$\sqrt{3}$<r<2,∴3<r2<4,
由r2+$\frac{12}{{r}^{2}}$≥2$\sqrt{{r}^{2}•\frac{12}{{r}^{2}}}$=4$\sqrt{3}$,
当且仅当r2=2$\sqrt{3}$∈(3,4),
|MN|取得最大值,且为$\sqrt{7-4\sqrt{3}}$=2-$\sqrt{3}$.
点评 本题考查椭圆的方程的求法,注意运用椭圆的焦半径公式和椭圆的范围,考查直线和圆相切的条件:d=r,直线和椭圆相切的条件:判别式为0,以及基本不等式的运用,考查化简整理的运算能力,属于难题.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
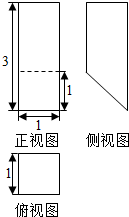
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
| 测试指标 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10) |
| 零件数 | 2 | 8 | 32 | 38 | 20 |
(2)生产一件零件,若是优质品可盈利40元,若是正品盈利20元,若是次品则亏损20元,若从大量的零件中随机抽取2件,其利润之和记为x(单位:元),求x的分布列及数学期望.
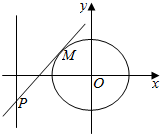 已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.
已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.